- Partimos da equação da força gravitacional:
\[
\boxed{F = G \frac{m_g M}{r^2}}
\]
Onde:
\(F\) é a força de atração gravitacional,
\(G\) é a constante gravitacional,
\(m_g\) é a massa gravitacional do corpo em queda,
\(M\) é a massa do corpo que atrai (por exemplo, a Terra),
\(r\) é a distância entre os centros de massa dos corpos.
De acordo com a Segunda Lei de Newton, temos:
\[
\boxed{F = m_i a}
\]
Onde:
Igualando as duas expressões de \(F\):
\[
m_i a = G \frac{m_g M}{r^2}
\]
Isolando \(a\):
\[
a = G \frac{m_g}{m_i} \cdot \frac{M}{r^2}
\]
- Agora, assumimos como postulado experimental a igualdade entre massa gravitacional e inercial:
\[
\boxed{m_g = m_i}
\]
Substituindo:
\[
\boxed{a = G \frac{M}{r^2}}
\]
Importante: Essa aceleração independe da massa do corpo que está caindo.
Isso explica por que uma pena e uma bola de chumbo caem com a mesma aceleração no vácuo, como demonstrado no experimento feito na Lua pela missão Apollo 15.
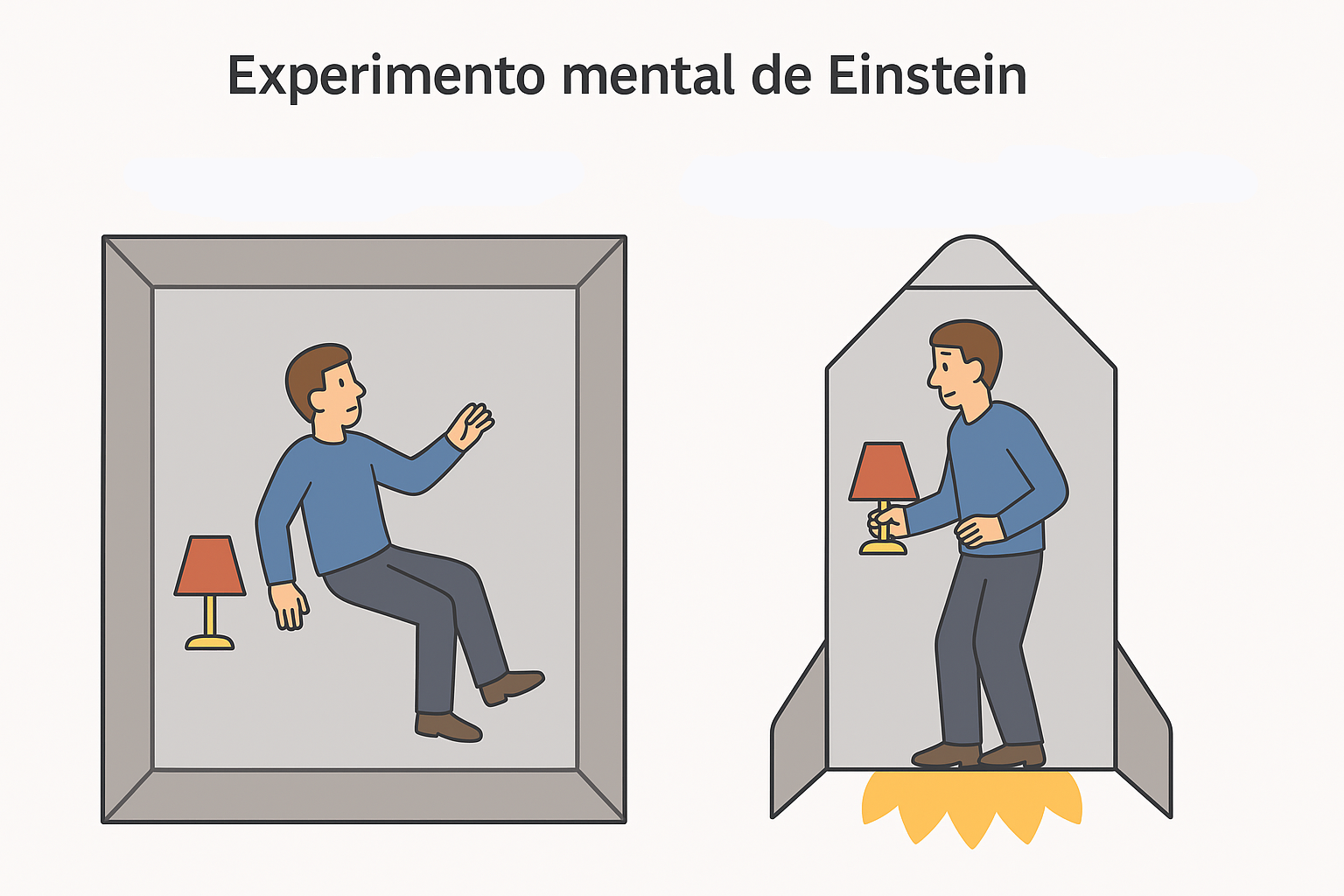
Essa igualdade \(m_g = m_i\) era conhecida desde Newton, mas foi verificada com altíssima precisão nos experimentos de Eötvös e outros. Mais tarde, Einstein elevou essa equivalência a um princípio fundamental da física moderna: o princípio da equivalência, pedra angular da teoria da relatividade geral.
- Equações do movimento
Suponha que soltemos dois corpos (a pena e a bola de chumbo) de uma mesma altura \(h\), com velocidade inicial zero.
No vácuo, um corpo em queda livre está sujeito unicamente à força gravitacional, o que faz com que sua aceleração seja constante e igual à aceleração da gravidade \(g\). Nesse contexto, o movimento é uniformemente acelerado, com aceleração constante \(a = g\), dirigida para baixo.
- Equação do movimento retilíneo uniformemente acelerado
De acordo com a cinemática clássica, a posição \(y(t)\) de um corpo em movimento retilíneo uniformemente acelerado é dada por:
\[
\boxed{y(t) = y_0 + v_0 t + \frac{1}{2} a t^2}
\]
onde:
\(y_0\) é a posição inicial,
\(v_0\) é a velocidade inicial,
\(a\) é a aceleração constante,
\(t\) é o tempo decorrido desde o início do movimento.
- Aplicação ao caso da queda livre
No caso da queda de um corpo solto do repouso:
A posição inicial é \(y_0 = h\),
A velocidade inicial é \(v_0 = 0\),
A aceleração é \(a = -g\), pois o eixo vertical é orientado para cima e a gravidade atua para baixo.
Substituindo esses valores na fórmula da posição:
\[
y(t) = h + 0 \cdot t + \frac{1}{2} (-g) t^2 = h - \frac{1}{2} g t^2
\]
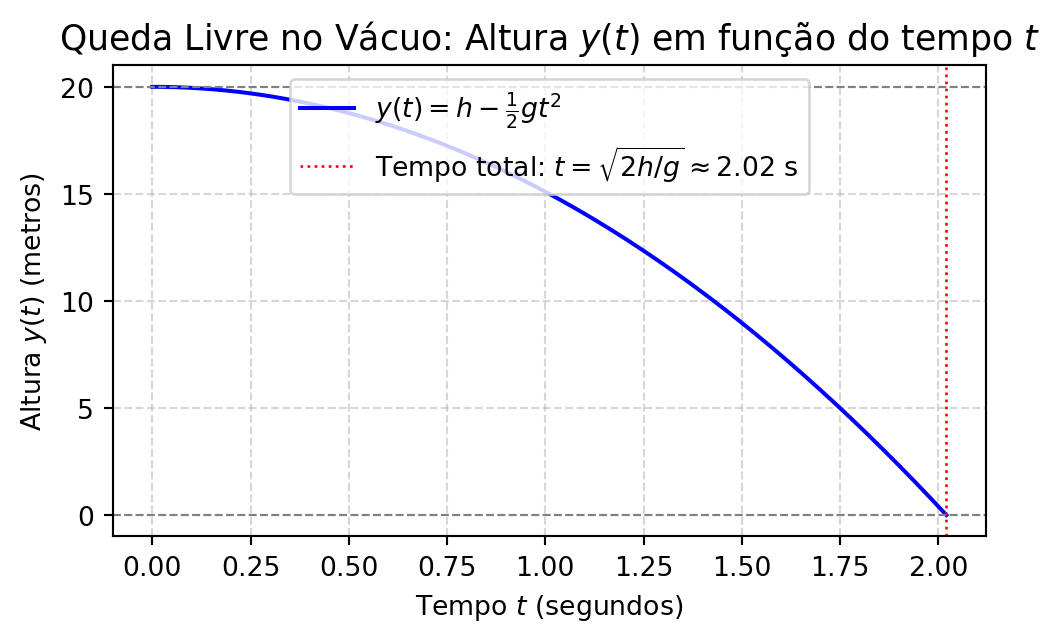
Portanto, a equação que descreve a posição vertical do corpo em queda livre no instante \(t\) é:
\[
\boxed{
y(t) = h - \frac{1}{2} g t^2
}
\]
- Interpretação física
O termo \(h\) representa a altura inicial de onde o corpo foi solto.
O termo \(\frac{1}{2} g t^2\) representa o quanto o corpo já “desceu” devido à aceleração da gravidade após o tempo \(t\).
A posição \(y(t)\) diminui com o tempo, até atingir o solo (\(y = 0\)).
Essa equação mostra claramente que o deslocamento é proporcional ao quadrado do tempo, característica típica de movimentos com aceleração constante.
- Considerando \(y=0\) como o solo, a queda termina quando \(y(t) = 0\):
\[
0 = h - \frac{1}{2} g t^2 \implies \frac{1}{2} g t^2 = h \implies t^2 = \frac{2h}{g}
\] \[
\implies t = \sqrt{\frac{2h}{g}}
\]
Ou seja, o tempo para o objeto atingir o solo é:
\[
\boxed{t = \sqrt{\frac{2h}{g}}}
\]
Importante: este tempo não depende da massa do objeto.
Como a pena e a bola de chumbo estão submetidas à mesma aceleração \(g\) e são soltas da mesma altura e com velocidade inicial zero, o tempo para atingirem o solo é o mesmo, dado por:
\[
\boxed{
t_{\text{pena}} = t_{\text{bola}} = \sqrt{\frac{2h}{g}}
}
\]
Portanto, no vácuo, pena e bola de chumbo chegam ao solo ao mesmo tempo.
Em meios com atmosfera, como na Terra, a pena cai mais devagar devido ao arrasto do ar, que depende da forma e da densidade do objeto. No vácuo, porém, esse efeito desaparece — e então o que prevalece é unicamente a aceleração gravitacional \(g\), que é a mesma para todos os corpos.