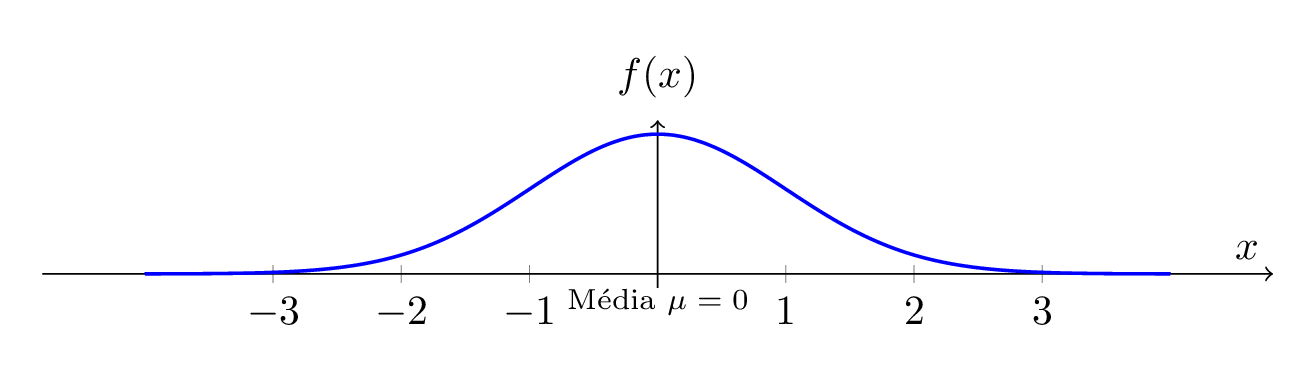🎓 📊 Curso de Estatística: A Distribuição Normal (Parte 1): Introdução à Distribuição Normal

estatística
distribuição normal
cursos
exercícios
Este curso tem como propósito apresentar, de forma acessível e aplicada, os fundamentos da distribuição normal, também conhecida como distribuição de Gauss, com apoio de visualizações gráficas e ferramentas computacionais.
Autor

Blog do Marcellini

Data de Publicação

24 de julho de 2025

· ← Sumário do Curso · ← Cursos de Estatística · ← Seção de Estatística

Distribuição Normal

1 🎓 📊 A Distribuição Normal — Parte 1

Este curso tem como propósito apresentar, de forma acessível e aplicada, os fundamentos da distribuição normal, também conhecida como distribuição de Gauss, com apoio de visualizações gráficas e ferramentas computacionais.

Nota📌 Objetivos do Post
  • A curva de Gauss e a Regra Empírica;
  • O conceito de escore-\(z\) e como usá-lo para calcular probabilidades;
  • A interpretação da área sob a curva e suas aplicações em situações reais;
  • Cálculos práticos com o uso da Tabela Z, R e Excel.
Nota🌱 Introdução: O que Estamos Estudando?

Antes de mergulhar na distribuição normal, é fundamental compreender alguns conceitos-chave da estatística. Eles fornecem a base para entender como podemos descrever e analisar dados no mundo real.

  • 🔢 População
    É o conjunto completo de elementos com uma característica de interesse.
    Exemplos: todos os alunos de uma escola, todas as lâmpadas produzidas por uma fábrica, ou todos os habitantes de um país.

  • 🧪 Amostra
    É um subconjunto da população, usado quando é inviável medir todos os elementos. Uma amostra bem escolhida permite fazer inferências sobre a população.
    Exemplo: medir o QI de 200 estudantes para estimar o QI médio da escola.

  • 🎲 Variável aleatória
    Representa um fenômeno incerto, cujos valores possíveis são associados a resultados numéricos.
    Pode ser:

    • Discreta: assume valores específicos e contáveis (número de filhos por família, chamadas atendidas por dia).
    • Contínua: assume qualquer valor dentro de um intervalo (altura, tempo, temperatura, QI).

  • 📊 Distribuição de probabilidade
    Mostra como os valores de uma variável aleatória estão distribuídos.
    Exemplos: a chance de um bebê nascer com determinado peso; a probabilidade de um carro consumir certa quantidade de combustível.

  • 📈 Função densidade de probabilidade (FDP)
    Para variáveis contínuas, usamos curvas em vez de tabelas. A altura da curva indica a probabilidade relativa de cada valor, e a área sob a curva representa a probabilidade total de um intervalo.
    Exemplo: a área entre 160 cm e 170 cm na curva da altura humana indica a proporção de pessoas nessa faixa.

  • ⚖️ Média (\(\mu\))
    Valor central da distribuição.
    Exemplo: se a média de estatura dos adultos é 170 cm, então esse é o ponto de equilíbrio da curva.

  • 📐 Desvio padrão (\(\sigma\))
    Mede a dispersão dos dados em torno da média. Quanto maior \(\sigma\), mais “espalhados” estão os dados.
    Exemplo: se a média de QI é 100 e \(\sigma = 15\), a maioria das pessoas terá QI entre 85 e 115.

Nota🌍 Importância da Distribuição Normal

A distribuição normal é um modelo estatístico essencial porque descreve com precisão muitos fenômenos do mundo real — tanto naturais quanto sociais. Ela surge, sobretudo, quando várias causas aleatórias e independentes influenciam um resultado final. Nessas situações, os dados tendem a se concentrar em torno de uma média, formando a clássica curva em forma de sino.

🔎 Por que isso importa?
Porque a normalidade simplifica a análise estatística e viabiliza o uso de ferramentas poderosas de inferência.

📌 Exemplos práticos:

  • 📚 Notas em provas padronizadas: os escores se distribuem em torno da média, com poucos alunos obtendo notas muito altas ou muito baixas.

  • 🌿 Altura de plantas de uma mesma espécie cultivadas sob condições semelhantes tende a se agrupar em torno de um valor central.

  • 📉 Retornos de ativos financeiros (ações, moedas) se aproximam de uma curva normal em períodos curtos — embora com ressalvas quanto a eventos extremos.

📈 Com a suposição de normalidade, podemos:

  • Calcular probabilidades com fórmulas e tabelas conhecidas;

  • Estimar intervalos de confiança;

  • Aplicar testes de hipóteses;

  • Visualizar dados de forma clara e comparável.

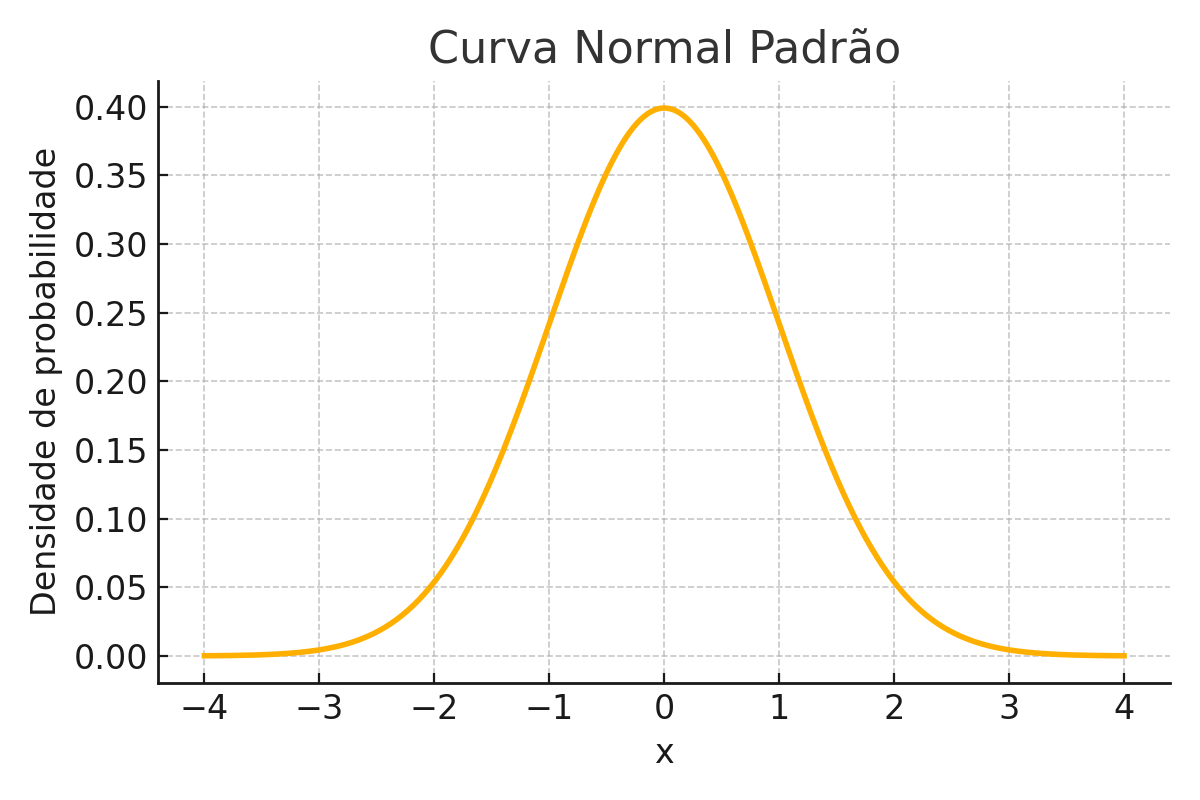
1.1 📏 Curva Normal Padrão

A curva normal, também conhecida como distribuição de Gauss, é uma das ferramentas mais fundamentais da estatística. Ela descreve como certas variáveis se distribuem em torno de uma média, com a maioria dos valores concentrados próximos a essa média e poucos valores em extremos.

Quando falamos da curva normal padrão, estamos nos referindo a uma versão específica dessa distribuição, com:

  • média \(\mu = 0\)
  • desvio padrão \(\sigma = 1\)

Essa padronização facilita a comparação entre diferentes conjuntos de dados e é a base para muitos procedimentos estatísticos, como cálculo de probabilidades, testes de hipóteses e construção de intervalos de confiança.

1.1.1 🧠 Por que ela é tão importante?

A curva normal padrão é usada para:

  • modelar fenômenos naturais (como altura, peso, erros de medição);
  • padronizar dados em escores z;
  • construir tabelas de referência;
  • desenvolver o raciocínio inferencial em estatística.

Nota

Curva Normal (ou Distribuição de Gauss):
Representa uma distribuição simétrica em torno da média.
Na versão padrão, a média é \(\mu = 0\) e o desvio padrão \(\sigma = 1\).
A área sob a curva corresponde à totalidade da população observada.

1.2 🎯 Medindo o Invisível

Nem sempre conseguimos observar diretamente as características de uma população. Em muitos casos, lidamos com conceitos abstratos — como inteligência, habilidade musical, produtividade ou motivação — que não podem ser medidos de forma direta e objetiva.

No entanto, mesmo sendo “invisíveis”, essas características deixam indícios nos dados: provas, testes, avaliações, questionários, desempenhos práticos. A estatística entra justamente nesse ponto: ajuda a inferir o que não vemos a partir daquilo que conseguimos medir.

  • Supõe-se, por exemplo, que essas características:
    • tendem a se concentrar em torno da média;
    • são raras nos extremos (valores muito altos ou muito baixos);
    • podem ser representadas por curvas simétricas, como a curva normal.
Dica

Estimar é medir com incerteza.
A curva normal nos oferece uma maneira de descrever essa incerteza com precisão matemática.

1.3 📐 A Curva Normal: Um Pouco Mais Fundo

A curva normal pode ser entendida como a representação gráfica de uma função matemática chamada função densidade de probabilidade.

  • O eixo horizontal representa os valores medidos da variável: \(x\).
  • O eixo vertical indica a altura da curva em cada ponto: \(f(x)\), ou seja, a densidade de probabilidade.
  • A relação entre \(x\) e \(f(x)\) é descrita por uma fórmula:

\[ \boxed{f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \cdot e^{-\frac{(x - \mu)^2}{2\sigma^2}}} \]

onde:

  • \(\mu\) é a média da distribuição,
  • \(\sigma\) é o desvio padrão,
  • \(e\) é a base do logaritmo natural (aproximadamente 2,718).

Na forma padrão, temos \(\mu = 0\) e \(\sigma = 1\).

  • Para cada valor de \(x\), a função retorna a altura da curva naquele ponto.
  • A área sob a curva entre dois valores representa a probabilidade de que a variável aleatória assuma um valor nesse intervalo.

1.4 📈 Representação Gráfica da Curva Normal

Nota

Curva Normal Padrão:
A curva é centrada em \(\mu = 0\) e o desvio padrão é \(\sigma = 1\).
A área sob a curva representa a distribuição da população em torno da média.

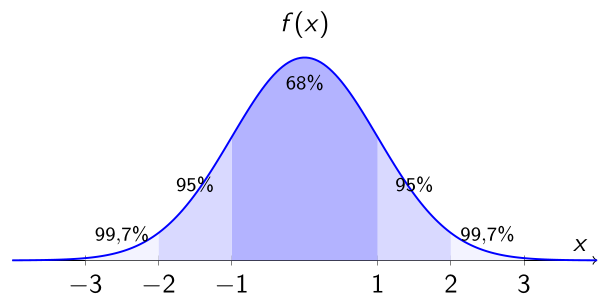
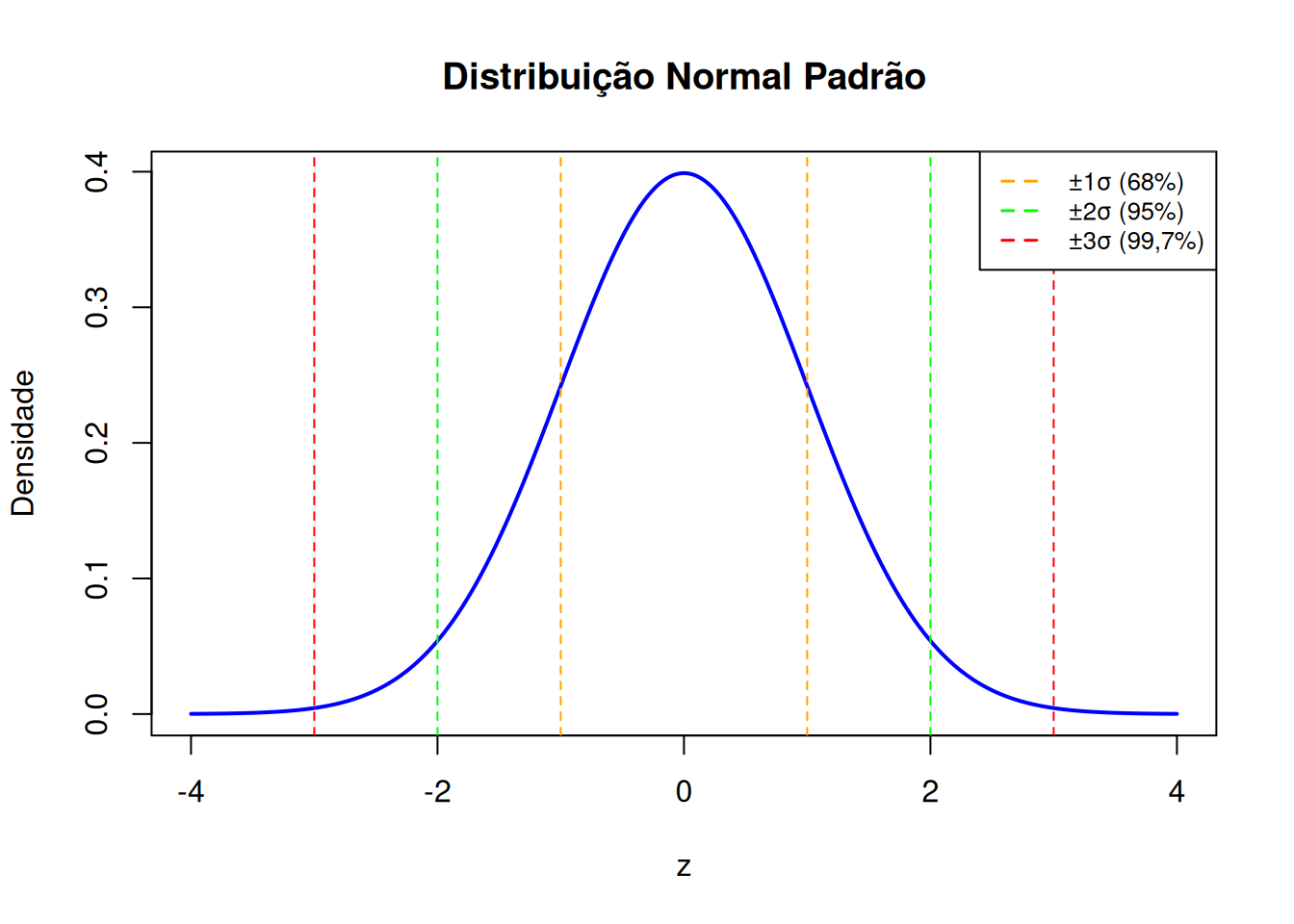
1.5 📏 Regra Empírica — 68% - 95% - 99,7%

A Regra Empírica descreve como os dados se distribuem em torno da média em uma distribuição normal padrão.

  • Cerca de 68% dos dados estão entre \(\mu - 1\sigma\) e \(\mu + 1\sigma\)
  • Cerca de 95% dos dados estão entre \(\mu - 2\sigma\) e \(\mu + 2\sigma\)
  • Cerca de 99,7% dos dados estão entre \(\mu - 3\sigma\) e \(\mu + 3\sigma\)

Nota

A Regra Empírica é uma ferramenta visual poderosa.
Permite identificar rapidamente o que é comum e o que é raro em uma população que segue uma distribuição normal.

1.6 📌 Parâmetros da Distribuição Normal

A distribuição normal não é uma curva única, mas sim uma família de curvas.
Cada membro dessa família é completamente descrito por dois parâmetros populacionais:

  • Média \(\mu\):
    Indica o centro da distribuição. A curva é simétrica em torno desse valor.

  • Desvio padrão \(\sigma\):
    Mede a dispersão dos dados.
    Curvas com maior \(\sigma\) são mais largas e achatadas; com menor \(\sigma\), são mais estreitas e altas.

Nota

Em qualquer distribuição normal, a curva é perfeitamente simétrica:
o lado esquerdo espelha exatamente o lado direito em relação à média.

1.6.1 🎯 Por que esses parâmetros são importantes?

Conhecendo \(\mu\) e \(\sigma\), podemos:

  • Localizar valores típicos da população;

  • Calcular probabilidades de ocorrerem valores em certos intervalos;

  • Padronizar dados de diferentes distribuições usando a transformação:

\[ \boxed{z = \frac{x - \mu}{\sigma}} \]

Essa transformação converte qualquer valor \(x\) em um escore-z, possibilitando o uso direto da distribuição normal padrão.

Nota

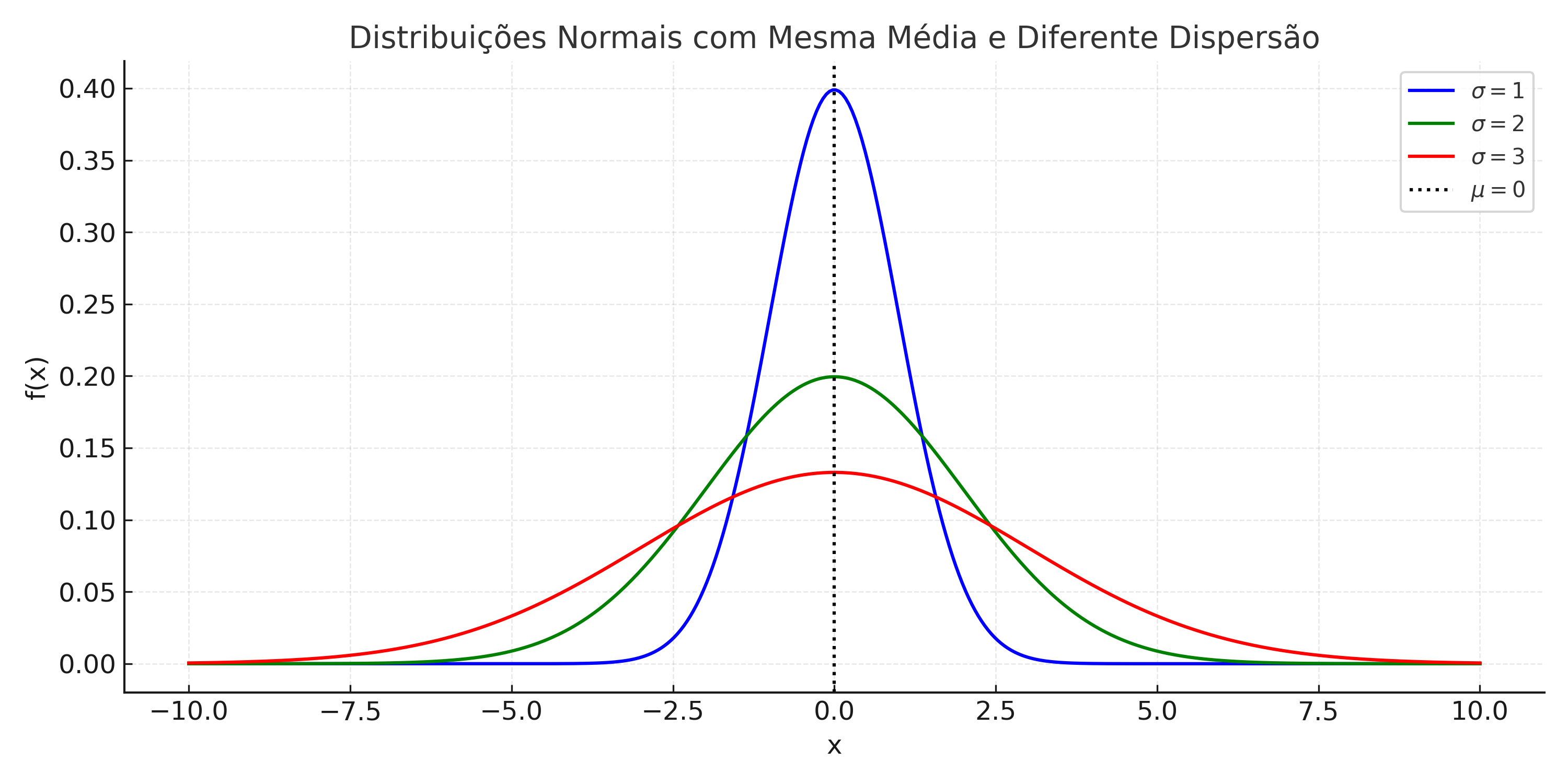
Curvas Normais com a Mesma Média
A média define a posição central das curvas.
A forma (altura e largura) é controlada exclusivamente pelo desvio padrão \(\sigma\).

1.7 🎓 Exemplo: Distribuição de QI (Stanford–Binet)

Vamos aplicar a distribuição normal em um caso prático.

Suponha que os escores de QI (Quociente de Inteligência) sigam uma distribuição normal com:

  • Média \(\mu = 100\)
  • Desvio padrão \(\sigma = 16\)

1.7.1 🧠 Interpretação

Nota

Intervalo de 1 Desvio Padrão em torno da Média

A fórmula geral para calcular esse intervalo é:

\[ \mu \pm k\sigma \]

Neste exemplo, com \(\mu = 100\), \(\sigma = 16\) e \(k = 1\):

\[ \mu - 1\sigma = 100 - 1 \times 16 = 84 \] \[ \quad \text{e} \quad \] \[ \mu + 1\sigma = 100 + 1 \times 16 = 116 \]

Portanto, segunda a Regra Empírica cerca de 68% da população tem QI entre 84 e 116.

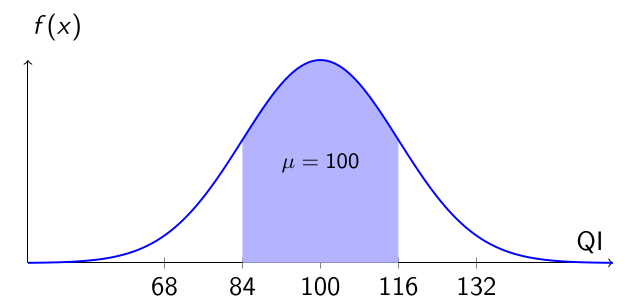
1.7.2 📊 Visualizando

Nota

Distribuição de QI — Intervalo de 1 Desvio Padrão

A área sombreada representa os indivíduos com QI entre 84 e 116.
Segundo a regra empírica, esse intervalo contém cerca de 68% da população.

1.7.3 💡 Conclusão

  • O teste Stanford–Binet é calibrado para seguir essa distribuição.
  • A curva normal permite avaliar o quão comum ou raro é um escore de QI.
  • Escores fora do intervalo \(\mu \pm 2\sigma\) (entre 68 e 132) já são considerados atípicos.
Nota

A distribuição normal é útil para comparar indivíduos à média da população e identificar desempenhos excepcionais.

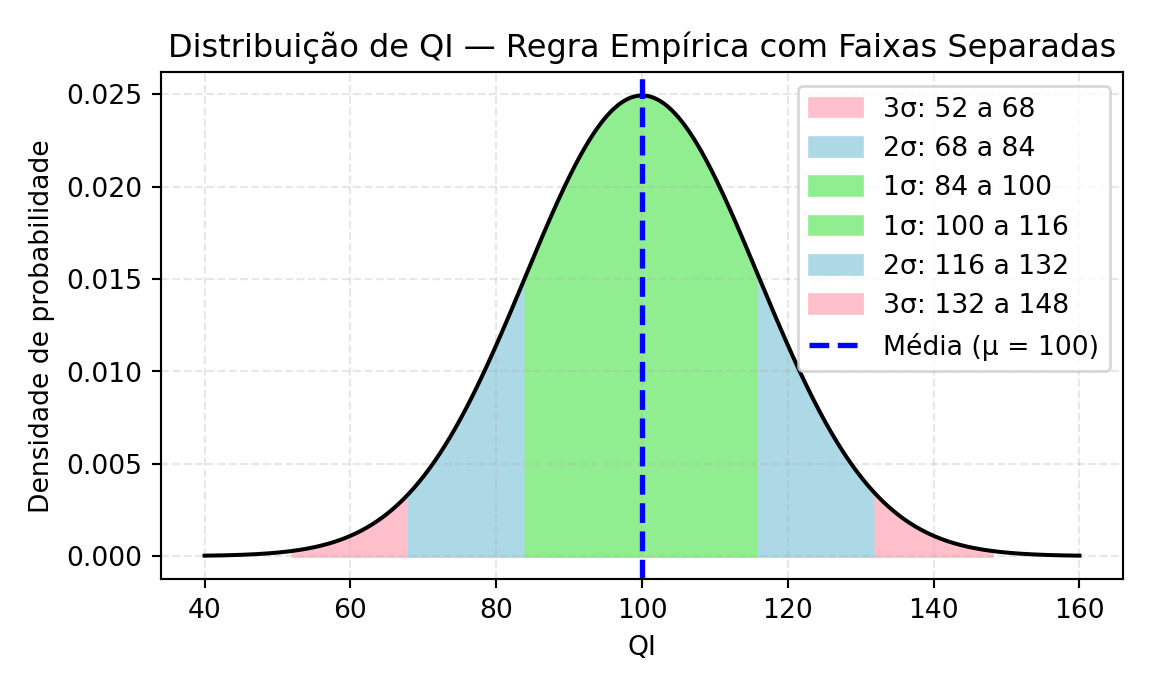
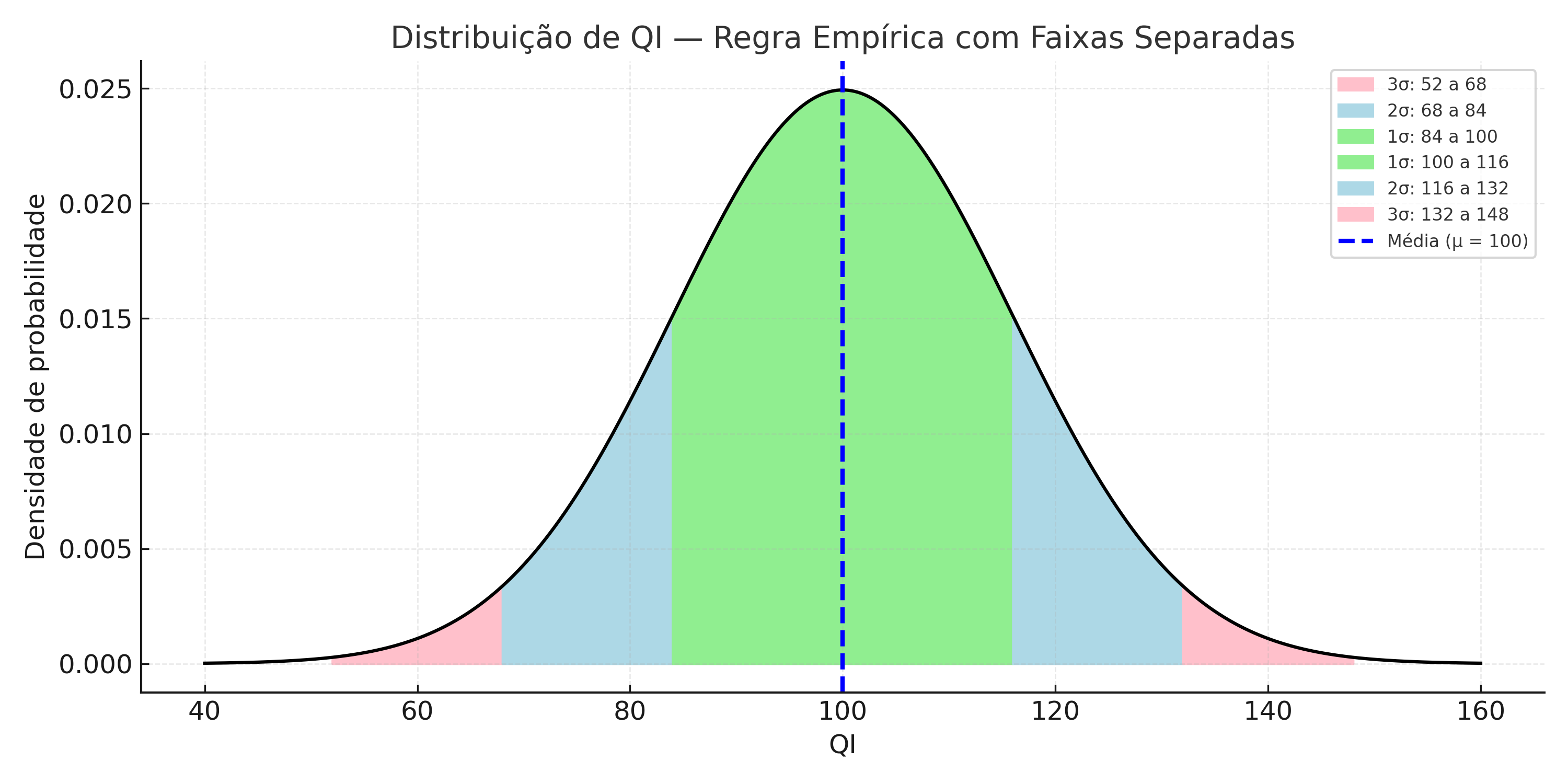
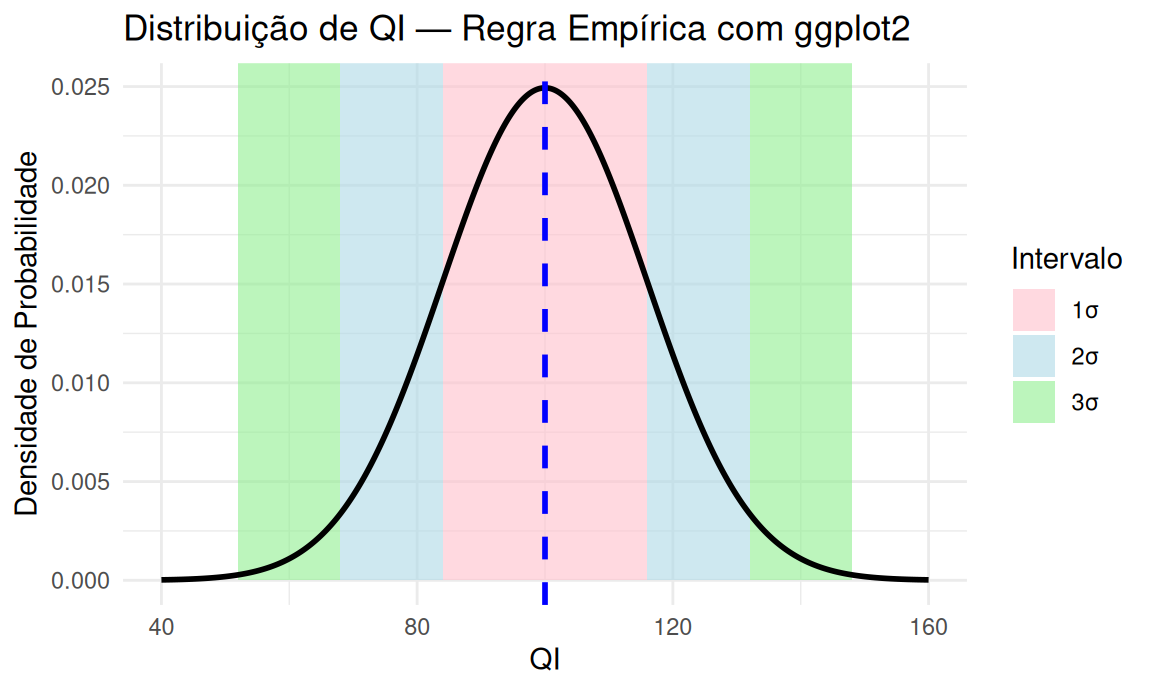
1.8 📐 Regra Empírica Aplicada à Distribuição de QI

Nota

Regra Empírica Aplicada ao QI

A distribuição de QI (com média \(\mu = 100\) e desvio padrão \(\sigma = 16\)) permite visualizar a Regra Empírica de forma clara:

  • 68% dos indivíduos têm QI entre 84 e 116 \((\mu \pm 1\sigma)\)
  • 95% estão entre 68 e 132 \((\mu \pm 2\sigma)\)
  • 99,7% estão entre 52 e 148 \((\mu \pm 3\sigma)\)

Cada faixa da curva representa uma porção da população e foi desenhada com cores não sobrepostas para destacar suas contribuições individuais.

1.9 🧪 Exemplo com Código Python: Visualizando a Regra Empírica

Vamos representar graficamente uma distribuição de QI usando a regra empírica. Suponha que os escores de QI sigam uma distribuição normal com média \(\mu = 100\) e desvio padrão \(\sigma = 16\). O gráfico abaixo mostra as faixas não sobrepostas da regra empírica:

import matplotlib.pyplot as plt
import numpy as np

# Parâmetros da distribuição
mu = 100
sigma = 16
x = np.linspace(40, 160, 1000)
y = 1 / (np.sqrt(2 * np.pi) * sigma) * np.exp(- (x - mu)**2 / (2 * sigma**2))

# Faixas separadas da regra empírica
faixas = [
    {'label': '3σ: 52 a 68',   'x1': mu - 3*sigma, 'x2': mu - 2*sigma, 'color': '#FFC0CB'},
    {'label': '2σ: 68 a 84',   'x1': mu - 2*sigma, 'x2': mu - 1*sigma, 'color': '#ADD8E6'},
    {'label': '1σ: 84 a 100',  'x1': mu - 1*sigma, 'x2': mu,           'color': '#90EE90'},
    {'label': '1σ: 100 a 116', 'x1': mu,           'x2': mu + 1*sigma, 'color': '#90EE90'},
    {'label': '2σ: 116 a 132', 'x1': mu + 1*sigma, 'x2': mu + 2*sigma, 'color': '#ADD8E6'},
    {'label': '3σ: 132 a 148', 'x1': mu + 2*sigma, 'x2': mu + 3*sigma, 'color': '#FFC0CB'}
]

# Criar figura (sem figsize para usar fig-width/fig-height do Quarto)
fig, ax = plt.subplots()
ax.plot(x, y, color='black')

# Preencher faixas
for faixa in faixas:
    x_fill = np.linspace(faixa['x1'], faixa['x2'], 500)
    y_fill = 1 / (np.sqrt(2 * np.pi) * sigma) * np.exp(- (x_fill - mu)**2 / (2 * sigma**2))
    ax.fill_between(x_fill, y_fill, color=faixa['color'], label=faixa['label'])

# Linha da média
ax.axvline(mu, color='blue', linestyle='--', linewidth=2, label='Média (μ = 100)')

# Personalização
ax.set_title('Distribuição de QI — Regra Empírica com Faixas Separadas')
ax.set_xlabel('QI')
ax.set_ylabel('Densidade de probabilidade')
ax.grid(True, linestyle="--", alpha=0.3)
ax.legend(loc='upper right')
plt.tight_layout()
plt.show()

Distribuição de QI — Regra Empírica com faixas separadas.
Nota

Este gráfico evidencia como os valores de QI estão distribuídos em torno da média, com áreas coloridas representando:

  • Verde claro: 68% dos indivíduos (84 a 116)
  • Azul claro: 27% dos indivíduos (68 a 84 e 116 a 132)
  • Rosa claro: 4,7% dos indivíduos (52 a 68 e 132 a 148)

A linha pontilhada azul marca a média populacional.

library(ggplot2)

# Parâmetros
mu <- 100
sigma <- 16

# Sequência de valores
x <- seq(40, 160, length.out = 1000)
y <- dnorm(x, mean = mu, sd = sigma)
df <- data.frame(x = x, y = y)

# Faixas da Regra Empírica
faixas <- data.frame(
  xmin = c(mu - 3*sigma, mu - 2*sigma, mu - sigma, mu, mu + sigma, mu + 2*sigma),
  xmax = c(mu - 2*sigma, mu - sigma, mu, mu + sigma, mu + 2*sigma, mu + 3*sigma),
  grupo = c("3σ", "2σ", "1σ", "1σ", "2σ", "3σ"),
  cor = c("#FFC0CB", "#ADD8E6", "#90EE90", "#90EE90", "#ADD8E6", "#FFC0CB")
)

# Gráfico
ggplot(df, aes(x, y)) +
  geom_rect(data = faixas,
            aes(xmin = xmin, xmax = xmax, ymin = 0, ymax = Inf, fill = grupo),
            inherit.aes = FALSE, alpha = 0.6) +
  scale_fill_manual(values = unique(faixas$cor)) +
  geom_line(color = "black", linewidth = 1) +
  geom_vline(xintercept = mu, color = "blue", linetype = "dashed", linewidth = 1) +
  labs(
    title = "Distribuição de QI — Regra Empírica com ggplot2",
    x = "QI",
    y = "Densidade de Probabilidade",
    fill = "Intervalo"
  ) +
  theme_minimal()

Distribuição de QI — Regra Empírica com ggplot2.
Nota

Neste gráfico, cada intervalo da curva normal representa uma proporção da população:

  • Rosa claro: 68,27% dos indivíduos entre \(\mu \pm 1\sigma\)
  • Azul claro: de 68,27% até 95,45% (entre \(\mu \pm 1\sigma\) e \(\mu \pm 2\sigma\))
  • Rosa claro: de 95,45% até 99,73% (entre \(\mu \pm 2\sigma\) e \(\mu \pm 3\sigma\))

O traço azul pontilhado indica a média \(\mu = 100\).

1.10 📐 Fundamento da Regra Empírica

A Regra Empírica baseia-se na forma simétrica da curva normal e nas áreas sob a curva, que representam probabilidades.

  • A área total sob a curva normal é igual a 1 (ou 100%).
  • Essa área representa a probabilidade de ocorrência de valores dentro de determinados intervalos.
  • Para simplificação dos cálculos, utiliza-se a distribuição normal padrão, com média \(\mu = 0\) e desvio padrão \(\sigma = 1\).
Dica

Na distribuição normal padrão, a probabilidade de um valor estar entre dois pontos \(a\) e \(b\) é dada pela integral da função densidade entre esses limites.

1.10.1 🔢 Função densidade da normal padrão

\[ \boxed{f(z) = \frac{1}{\sqrt{2\pi}}\, e^{-z^2/2}} \]

\[ \boxed{P(a < Z < b) = \int_{a}^{b} f(z)\, dz} \]

Com base nessa função, obtemos as seguintes aproximações:

  • \(P(-1 < Z < 1) \approx 68{,}27\%\)
  • \(P(-2 < Z < 2) \approx 95{,}45\%\)
  • \(P(-3 < Z < 3) \approx 99{,}73\%\)

Essas porcentagens dão origem à famosa Regra 68–95–99,7, usada em estatística descritiva e inferência para avaliar a dispersão de dados ao redor da média em distribuições aproximadamente normais.

Nota

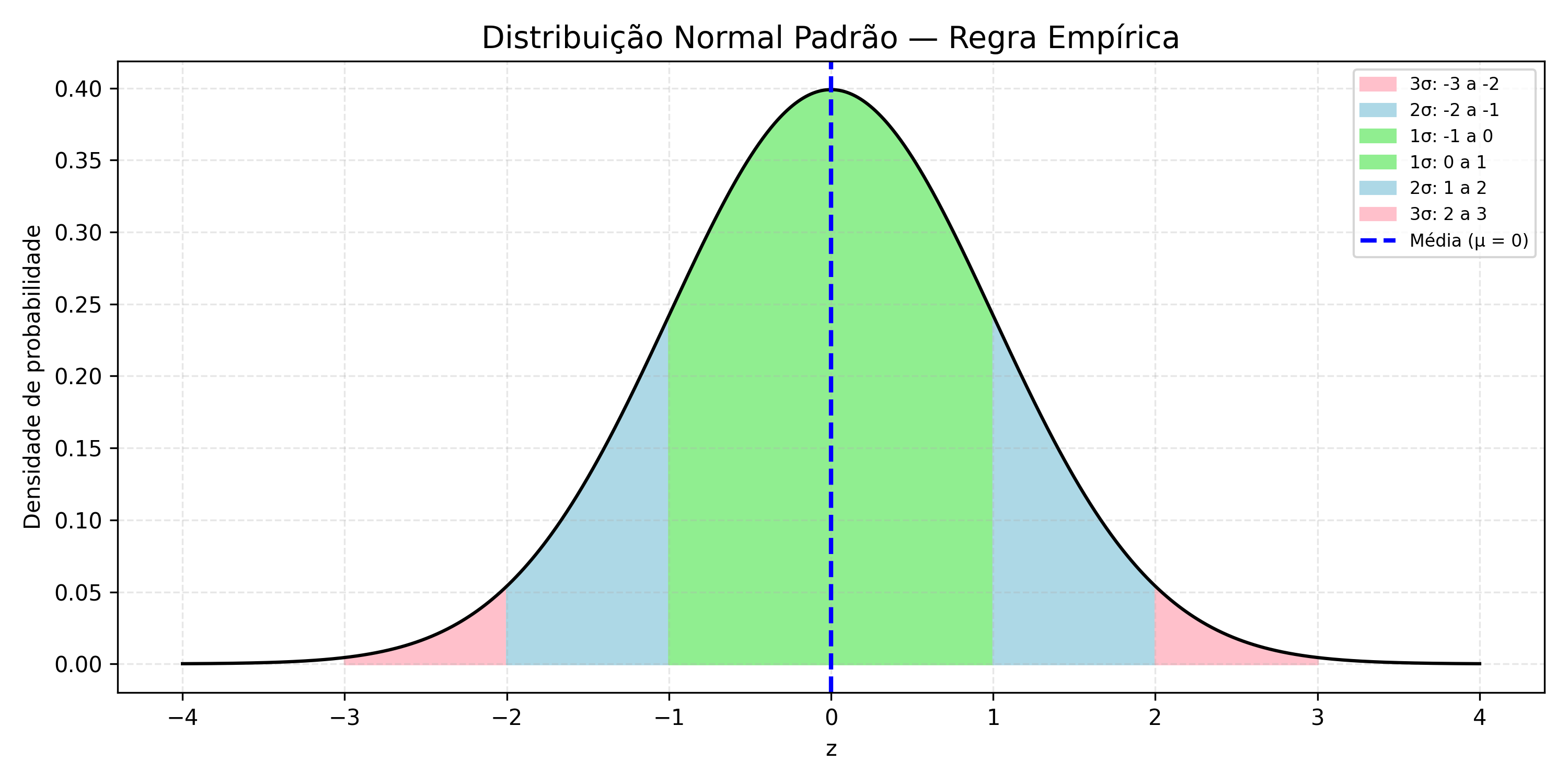
Distribuição Normal Padrão e a Regra Empírica

A imagem ilustra as faixas simétricas em torno da média \(\mu = 0\):

  • 68,27% dos valores entre \(-1\) e \(+1\) desvio padrão;
  • 95,45% entre \(-2\) e \(+2\);
  • 99,73% entre \(-3\) e \(+3\).

A área sob a curva representa a probabilidade do valor \(Z\) estar nesse intervalo.

1.11 Funções para Distribuição Normal: Excel e R

Podemos calcular probabilidades, valores acumulados e gerar gráficos com funções específicas:

NotaNo Excel

  • NORM.DIST(x, média, desvio_padrão, cumulativo)
    → Retorna a densidade ou a probabilidade acumulada da distribuição normal.

  • NORM.S.DIST(z, cumulativo)
    → Função específica para a distribuição normal padrão.

  • NORM.INV(probabilidade, média, desvio_padrão)
    → Retorna o valor de \(x\) associado a uma probabilidade acumulada.

  • NORM.S.INV(probabilidade)
    → Retorna o valor \(z\) na distribuição normal padrão.

NotaNo R

  • dnorm(x, mean, sd)
    → Retorna a densidade de probabilidade em \(x\).

  • pnorm(x, mean, sd)
    → Retorna a probabilidade acumulada até \(x\).

  • qnorm(p, mean, sd)
    → Retorna o quantil \(x\) tal que \(P(X \leq x) = p\).

  • rnorm(n, mean, sd)
    → Gera uma amostra aleatória de tamanho \(n\).

Dica

Observação: no Excel, cumulativo = VERDADEIRO retorna a probabilidade acumulada; FALSO retorna a densidade.

1.12 Exemplo Prático com R

Vamos visualizar a curva da distribuição normal padrão \(N(0, 1)\) e destacar as faixas de 1, 2 e 3 desvios-padrão da média — conhecidas pela Regra Empírica.

# Sequência de valores z
x <- seq(-4, 4, length.out = 1000)
y <- dnorm(x)

# Gerar o gráfico
plot(x, y, type = "l", lwd = 2, col = "blue",
     xlab = "z", ylab = "Densidade",
     main = "Distribuição Normal Padrão")

# Marcar as regiões da Regra Empírica
abline(v = c(-1, 1), col = "orange", lty = 2)
abline(v = c(-2, 2), col = "green", lty = 2)
abline(v = c(-3, 3), col = "red", lty = 2)

# Legenda
legend("topright",
       legend = c("±1σ (68%)", "±2σ (95%)", "±3σ (99,7%)"),
       col = c("orange", "green", "red"),
       lty = 2, lwd = 1.5, cex = 0.8)

Distribuição Normal Padrão com marcações de ±1σ, ±2σ e ±3σ

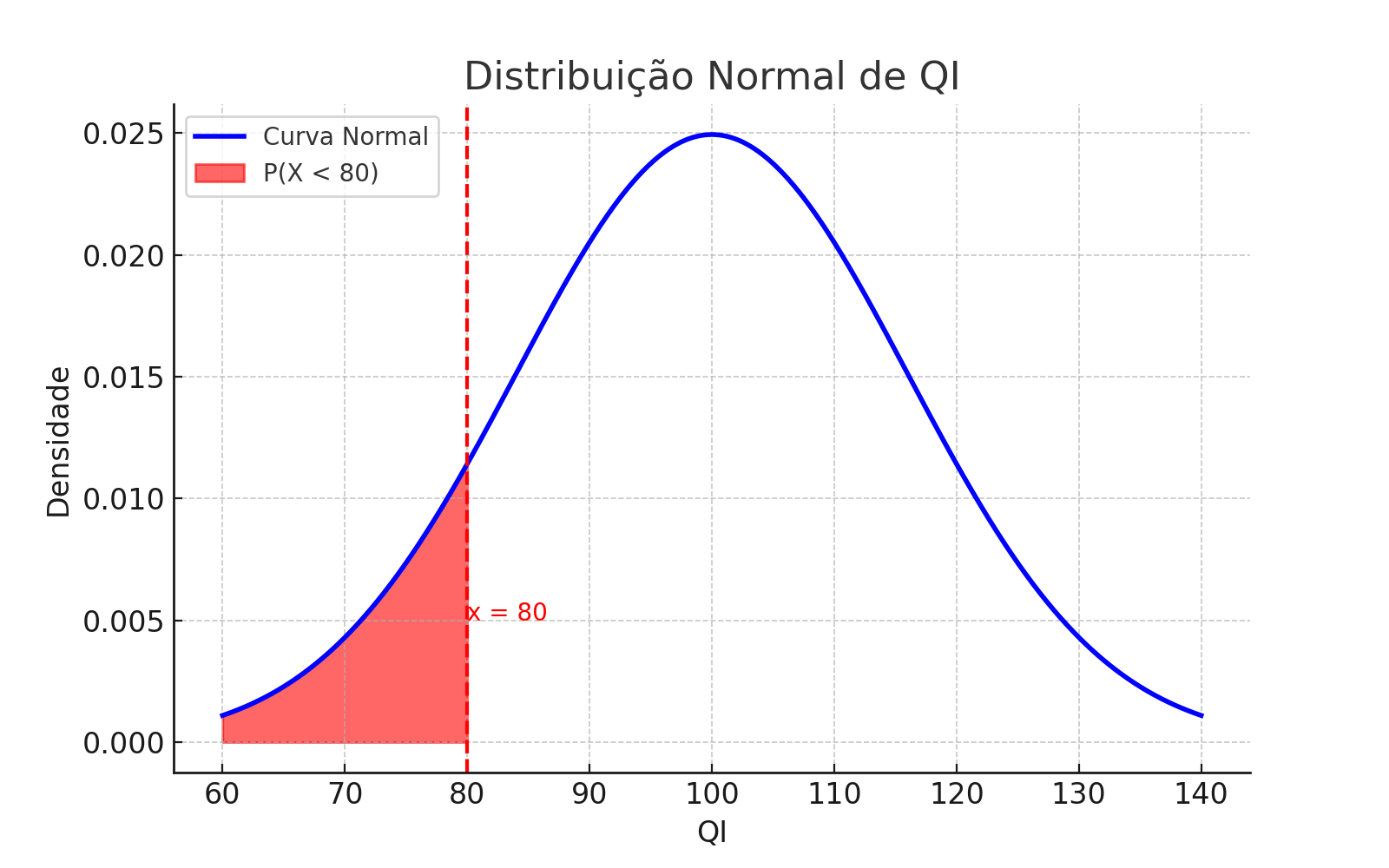
1.13 Exemplo Prático – Probabilidade de QI abaixo de 120

Problema: Qual a probabilidade de que uma pessoa tenha QI menor que 120?

Suponha que os QIs sigam uma distribuição normal com média \(\mu = 100\) e desvio padrão \(\sigma = 16\).
Queremos calcular:

\[ P(X < 120) \]

NotaNo Excel

=NORM.DIST(120; 100; 16; VERDADEIRO)
Resultado: \(\approx 0{,}8944\) ou 89,44%

NotaNo R

pnorm(120, mean = 100, sd = 16)
Resultado: \(\approx 0.8944\) ou 89,44%

Interpretação: aproximadamente 89,44% da população possui QI abaixo de 120, de acordo com a distribuição normal assumida.

1.14 Exemplo: Resolvendo sem Excel ou R — Usando o Escore-\(z\)

Queremos calcular a probabilidade de que uma pessoa tenha QI inferior a 120, assumindo que os QIs seguem uma distribuição normal com:

  • Média \(\mu = 100\)
  • Desvio padrão \(\sigma = 16\)

Desejamos encontrar:

\[ P(X < 120) \]

1.14.1 🧮 Passo 1: Padronização com o escore-\(z\)

Para usar a tabela da distribuição normal padrão, devemos primeiro padronizar o valor observado (120):

\[ z = \frac{x - \mu}{\sigma} = \frac{120 - 100}{16} = 1{,}25 \]

1.14.2 📖 Passo 2: Consulta à Tabela Z

Agora usamos a tabela da normal padrão \(Z \sim N(0,1)\) para encontrar \(P(Z < 1{,}25)\):

z 0.00 0.01 0.02 0.03 0.04 0.05
1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944

Tabela Z: \(P(Z < 1{,}25) = 0{,}8944\)

Cerca de 89,44% da população tem QI menor que 120, de acordo com a tabela da distribuição normal padrão.

1.15 📏 Entendendo o Escore-\(z\)

O escore-\(z\) é uma padronização que transforma qualquer valor \(x\) de uma distribuição normal \(N(\mu, \sigma^2)\) em um valor na distribuição normal padrão \(N(0, 1)\), com média 0 e desvio padrão 1.

Ele nos diz quantos desvios padrão o valor \(x\) está acima ou abaixo da média \(\mu\).

A fórmula é:

\[ \boxed{z = \frac{x - \mu}{\sigma}} \]

1.15.1 🔍 Interpretação:

  • Se \(z = 0\): o valor \(x\) está exatamente na média \(\mu\).
  • Se \(z > 0\): o valor \(x\) está acima da média.
  • Se \(z < 0\): o valor \(x\) está abaixo da média.

1.15.2 🎯 Por que é útil?

O escore-\(z\) unifica diferentes distribuições numa forma padrão, permitindo que possamos:

  • Consultar a Tabela Z da normal padrão \(N(0,1)\);
  • Calcular probabilidades acumuladas com facilidade;
  • Comparar valores entre distribuições com médias e desvios diferentes.

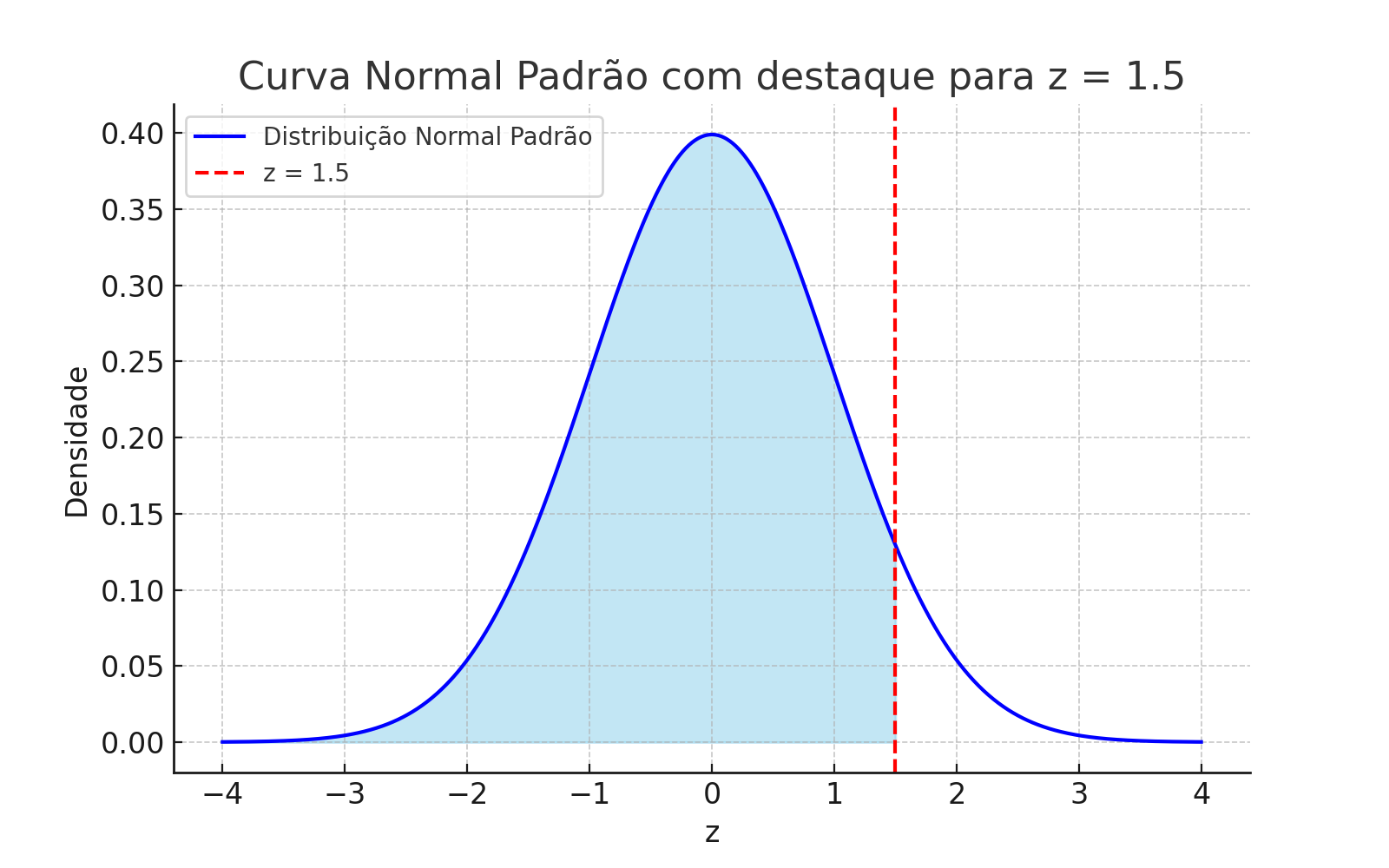
1.15.3 📊 Resumo Visual: Interpretando o Escore-\(z\)

Suponha que \(x = 124\), com média \(\mu = 100\) e desvio padrão \(\sigma = 16\).
O escore-\(z\) é calculado como:

\[ z = \frac{x - \mu}{\sigma} = \frac{124 - 100}{16} = 1{,}5 \]

Esse valor representa a posição relativa de \(x\) em uma distribuição normal padrão.

1.15.3.1 🔹 Área acumulada até \(z = 1{,}5\)

Área até z = 1,5

Aproximadamente 93,32% dos valores estão abaixo de \(x = 124\).

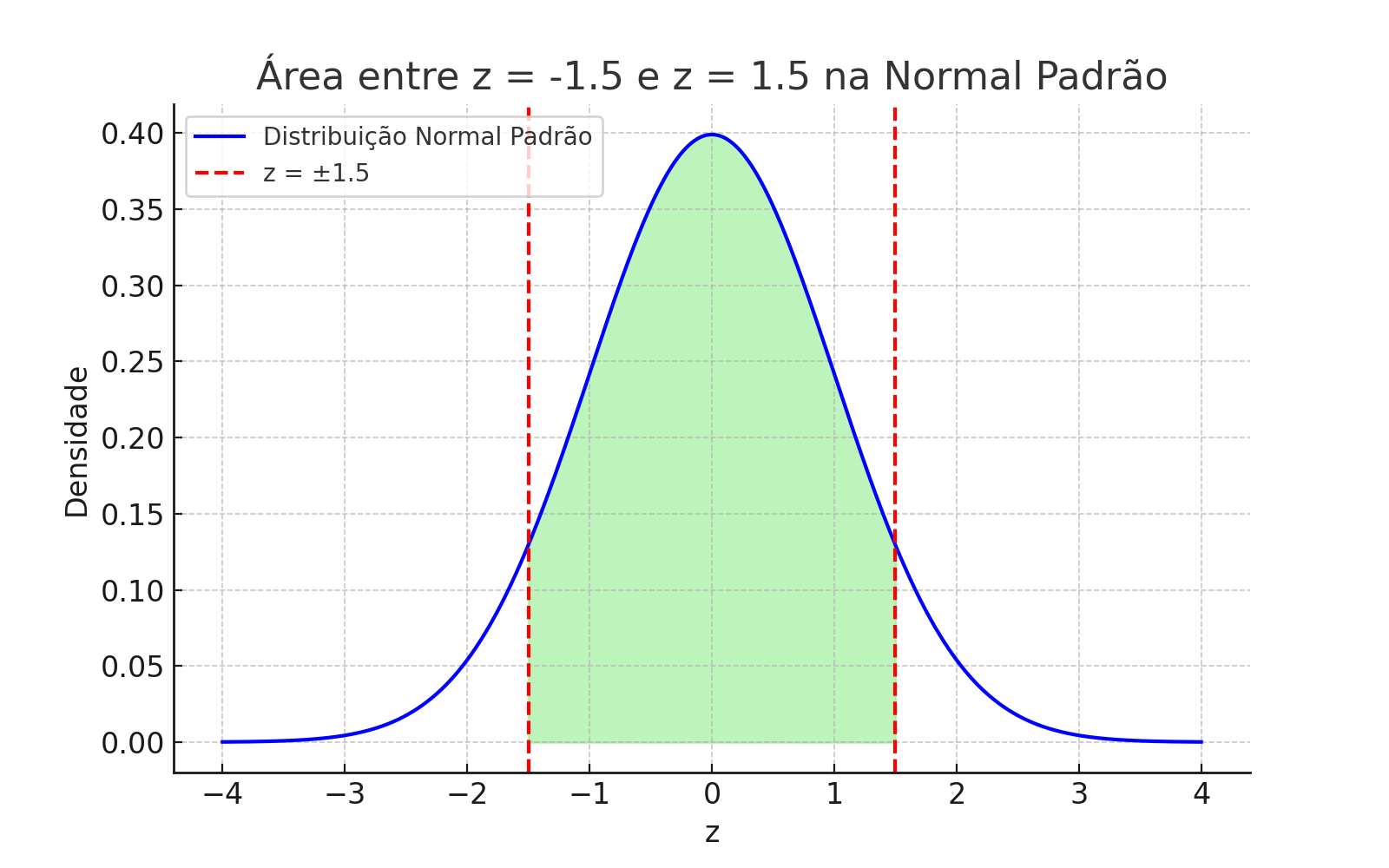
1.15.3.2 🔹 Área entre \(-1{,}5 < Z < 1{,}5\)

Área entre -1,5 e 1,5

Aproximadamente 86,64% dos valores estão a até 1,5 desvios da média, em ambos os lados.

1.15.3.3 🔹 Área à direita de \(z = 1{,}5\)

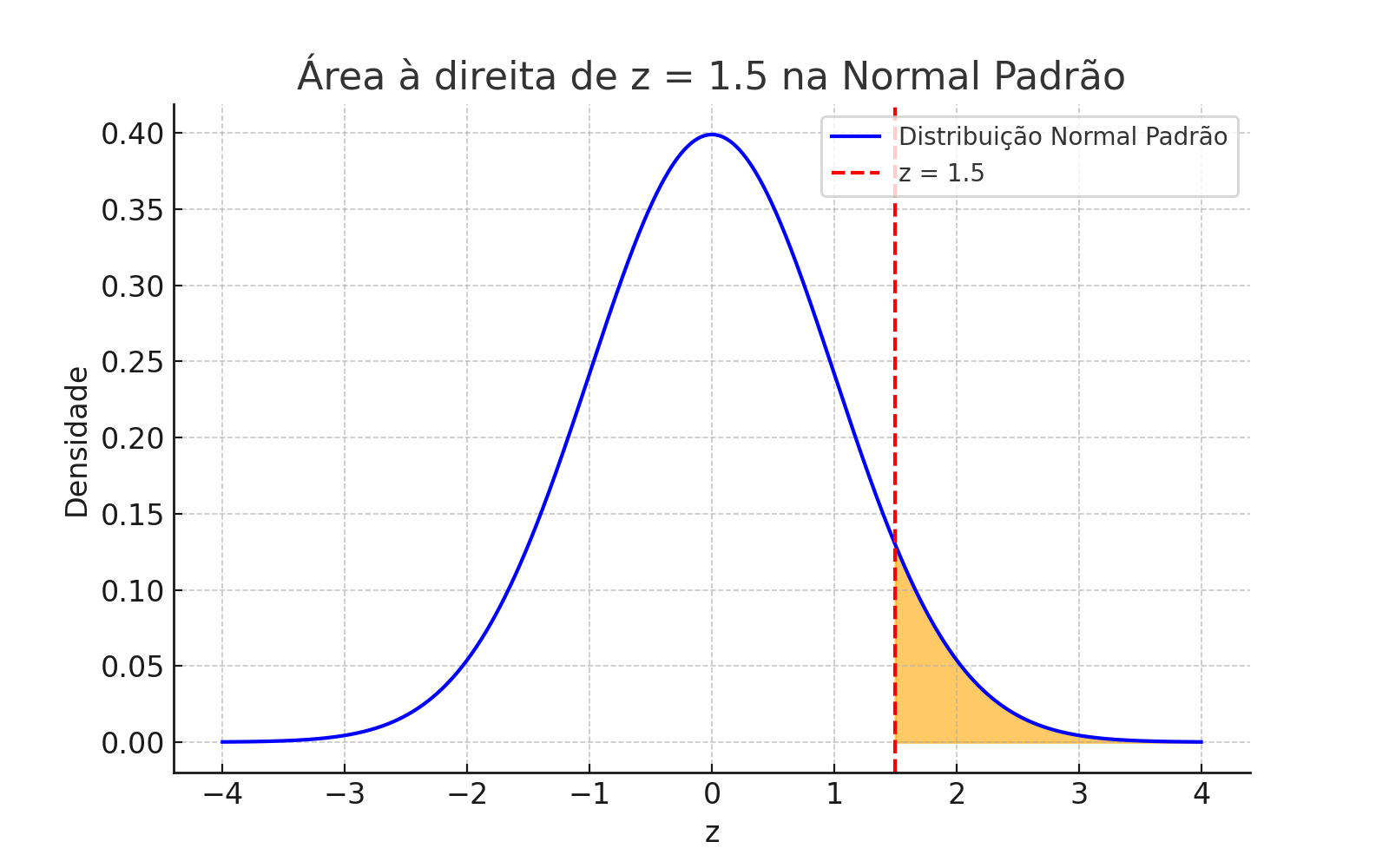
Área à direita de z = 1,5

Apenas 6,68% da distribuição está acima de \(x = 124\).

1.15.3.4 ✅ Conclusão

O escore-\(z\) permite:

  • Padronizar valores de diferentes distribuições;
  • Calcular probabilidades usando a Tabela Z ou software;
  • Visualizar a posição relativa de um valor em relação à média.

💡 Resumo Essencial:

\[ \boxed{z = \frac{x - \mu}{\sigma}} \]

Essa fórmula é a ponte entre qualquer valor \(x\) de uma distribuição normal e sua posição padronizada na curva \(N(0,1)\).

1.16 🧮 Cálculos com Tabela Z, R e Excel

A seguir, apresentamos os cálculos usados nos três exemplos do escore-\(z\), reforçando os gráficos anteriores. Mostramos como resolver com:

  • 📖 Tabela Z
  • 💻 R
  • 📊 Excel

1.16.1 🔹 Exemplo 1 — Área acumulada até \(z = 1{,}5\)

Queremos calcular:
\[ P(Z < 1{,}5) \]

🔎 Tabela Z — Linha 1.5, coluna 0.00:

z 0.00 0.01 0.02 0.03 0.04 0.05
1.5 0.9332 0.9336 0.9340 0.9345 0.9349 0.9353

Resultado: \[ P(Z < 1{,}5) = \boxed{0{,}9332} \]

💻 No R:

pnorm(1.5)
# [1] 0.9331928

📊 No Excel:

=NORM.S.DIST(1,5; VERDADEIRO)

Resultado: 0,9332

1.16.2 🔹 Exemplo 2 — Área entre \(-1{,}5 < Z < 1{,}5\)

Queremos calcular: \[ P(-1{,}5 < Z < 1{,}5) = \] \[ = P(Z < 1{,}5) - P(Z < -1{,}5) \]

🔎 Tabela Z:

  • \(P(Z < 1{,}5) = 0{,}9332\)
  • Pela simetria:
    \(P(Z < -1{,}5) = 1 - 0{,}9332 = 0{,}0668\)

Resultado: \[ P(-1{,}5 < Z < 1{,}5) = 0{,}9332 - 0{,}0668 = \boxed{0{,}8664} \]

💻 No R:

pnorm(1.5) - pnorm(-1.5)
# [1] 0.8663856

📊 No Excel:

=NORM.S.DIST(1,5; VERDADEIRO) - NORM.S.DIST(-1,5; VERDADEIRO)

Resultado: 0,8664

1.16.3 🔹 Exemplo 3 — Área à direita de \(z = 1{,}5\)

Queremos calcular: \[ P(Z > 1{,}5) = 1 - P(Z < 1{,}5) \]

🔎 Tabela Z:

\[ P(Z > 1{,}5) = 1 - 0{,}9332 = \boxed{0{,}0668} \]

💻 No R:

1 - pnorm(1.5)
# [1] 0.0668072

📊 No Excel:

=1 - NORM.S.DIST(1,5; VERDADEIRO)

Resultado: 0,0668

Esses cálculos mostram como o escore-\(z\) conecta valores observados a probabilidades em diferentes ferramentas — seja com a Tabela Z tradicional, ou com cálculo automatizado via R ou Excel.

1.17 🧾 Quadro-Resumo — Cálculos com Escore-\(z\)

1.17.1 🔵 Área até \(z = 1{,}5\)

  • Cálculo: \(P(Z < 1{,}5)\)
  • Resultado: 0,9332
  • R: pnorm(1.5)
  • Excel: =NORM.S.DIST(1,5; VERDADEIRO)

1.17.2 🟢 Área entre \(-1{,}5 < Z < 1{,}5\)

  • Cálculo: \(P(-1{,}5 < Z < 1{,}5)\)
  • Resultado: 0,8664
  • R: pnorm(1.5) - pnorm(-1.5)
  • Excel: =NORM.S.DIST(1,5; VERDADEIRO) - NORM.S.DIST(-1,5; VERDADEIRO)

1.17.3 🔴 Área à direita de \(z = 1{,}5\)

  • Cálculo: \(P(Z > 1{,}5)\)
  • Resultado: 0,0668
  • R: 1 - pnorm(1.5)
  • Excel: =1 - NORM.S.DIST(1,5; VERDADEIRO)

📌 Observação: Os resultados apresentados foram arredondados para 4 casas decimais, conforme a Tabela Z tradicional. Pequenas diferenças podem ocorrer nos softwares por causa da precisão interna das funções.

1.18 🔄 Encontrando o Valor Original \(x\) a Partir de um Escore-\(z\)

Podemos também fazer o processo inverso da padronização:

  • Se conhecemos:
    • o escore-\(z\)
    • a média \(\mu\)
    • e o desvio padrão \(\sigma\)

então podemos recuperar o valor original \(x\) da variável.

1.18.1 🧮 Fórmula Inversa

\[ \boxed{x = \mu + z \cdot \sigma} \]

1.18.2 ✏️ Exemplo

Qual o valor correspondente a \(z = 1{,}5\), com \(\mu = 100\) e \(\sigma = 16\) ?

Aplicando a fórmula:

\[ x = 100 + 1{,}5 \times 16 = 124 \]

✅ Conclusão: Um escore-\(z\) de 1,5 corresponde ao valor \(x=124\) nessa distribuição.

1.19 🧠 Exemplo: com Escore-\(z\) Negativo

Suponha que os escores de QI sigam uma distribuição normal com:

  • Média: \(\mu = 100\)
  • Desvio padrão: \(\sigma = 16\)
  • Objetivo: Qual a probabilidade de uma pessoa ter QI inferior a 80?

1.19.1 🧮 Passo 1 — Padronização:

\[ z = \frac{80 - 100}{16} = \frac{-20}{16} = -1{,}25 \]

1.19.2 📖 Passo 2 — Consulta à Tabela Z:

Como a tabela Z fornece valores para \(P(Z < z)\) com \(z\) positivo, usamos a simetria:

\[ P(Z < -1{,}25) = 1 - P(Z < 1{,}25) = \] \[ = 1 - 0{,}8944 = 0{,}1056 \]

Linha usada na tabela Z (linha 1.2, coluna 0.05):

\(z\) 0.00 0.01 0.02 0.03 0.04 0.05
1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944

1.19.3 🧪 Usando o R:

# Probabilidade de QI < 80
pnorm(80, mean = 100, sd = 16)
# Resultado: 0.1056498

1.19.4 🧮 Usando o Excel:

=NORM.DIST(80; 100; 16; VERDADEIRO)

Retorna: 0,1056498 → Aproximadamente 10,56%

1.19.5 📊 Visualização Gráfica

Distribuição Normal com área destacada para \(P(X < 80)\)

1.19.6 ✅ Conclusão

Cerca de \(\mathbf{10{,}56\%}\) da população tem QI inferior a 80, o que corresponde a estar 1,25 desvios padrão abaixo da média.

1.20 🔄 Visualizando \(P(Z < -1{,}25)\) com Simetria

A distribuição normal padrão é simétrica em torno de \(z = 0\).
Isso significa que as áreas abaixo da curva, à mesma distância da média, são iguais:

  • A área à esquerda de \(z = -1{,}25\) é igual à área à direita de \(z = 1{,}25\).
  • Assim, podemos escrever:

\[ P(Z < -1{,}25) = P(Z > 1{,}25) \]

E como:

\[ P(Z > 1{,}25) = 1 - P(Z < 1{,}25) \]

Concluímos que:

\[ P(Z < -1{,}25) = 1 - P(Z < 1{,}25) \]

Distribuição normal padrão: simetria entre \(P(Z < -1{,}25)\) e \(P(Z > 1{,}25)\)

1.21 📊 Exemplo Numérico com Simetria

Vamos calcular a probabilidade de uma pessoa ter QI inferior a 80, sabendo que:

  • A distribuição dos escores de QI é normal, com \(\mu = 100\) e \(\sigma = 16\)
  • Queremos: \(P(X < 80)\)

1.21.1 🧮 Passo 1 — Padronização

\[ z = \frac{80 - 100}{16} = -1{,}25 \]

1.21.2 📈 Passo 2 — Usando a Simetria e a Tabela Z

Sabemos que:

\[ P(Z < -1{,}25) = 1 - P(Z < 1{,}25) \]

E da Tabela Z:

Linha z = 1.2 | Coluna 0.05 →  
→ P(Z < 1.25) = 0.8944

Logo:

\[ P(Z < -1{,}25) = 1 - 0{,}8944 = 0{,}1056 \]

✅ Conclusão: Cerca de 10,56% da população tem QI inferior a 80.

1.21.3 🧪 Cálculo no R

# Média e desvio padrão
mu <- 100
sigma <- 16

# Probabilidade de QI < 80
pnorm(80, mean = mu, sd = sigma)
# Resultado: 0.1056498

1.21.4 📊 Cálculo no Excel

Use a fórmula:

=NORM.DIST(80; 100; 16; VERDADEIRO)

👉 Resultado: 0,1056498 (ou aproximadamente 10,56%)

🧠 Resumo:
Este exemplo mostra como a simetria da distribuição normal e a padronização via escore-\(z\) nos permitem calcular rapidamente a probabilidade de valores abaixo da média — inclusive com o apoio de ferramentas como Tabela Z, R e Excel.

1.22 📌 Conclusão da Parte 1: Introdução à Distribuição Normal

A Parte 1 do curso explorou os principais fundamentos da distribuição normal, incluindo:

  • A curva de Gauss e a Regra Empírica;
  • O conceito de escore-\(z\) e como usá-lo para calcular probabilidades;
  • A interpretação da área sob a curva e suas aplicações em situações reais;
  • Cálculos práticos com o uso da Tabela Z, R e Excel.

Com esse conhecimento, você já está apto a compreender fenômenos que seguem (ou se aproximam) de uma distribuição normal.

2 📚 Referências

  • Schmuller, Joseph. Statistical Analysis with Excel® For Dummies®, 5ª ed. Wiley, 2016.
  • Schmuller, Joseph. Análise Estatística com R Para Leigos, 2ª ed. Alta Books, 2021.
  • Levine, D. M.; Stephan, D.; Szabat, K. A. Statistics for Managers Using Microsoft Excel, 8ª ed. Pearson, 2017.
  • Morettin, L. G. Estatística Básica: Probabilidade e Inferência, 7ª ed. Pearson, 2017.
  • Morettin, P. A.; Bussab, W. O. Estatística Básica, 10ª ed. SaraivaUni, 2023.

3 🔗 Acesso Rápido às Partes do Curso

🎯 Parte 1: Introdução à Distribuição Normal (👉 você está aqui!)
🎯 Parte 2: Escore-z e Tabela Z
🎯 Parte 3: Gráficos, TCL e Normalidade Aproximada

· ← Sumário do Curso · ← Cursos de Estatística · ← Seção de Estatística · 🔝 Topo

Blog do Marcellini — Explorando a Estatística com Rigor e Beleza.

Nota

📌 Criado por Blog do Marcellini com ❤️ e código.