🎓📊 Distribuição Normal — Parte 2: Escore-z e Tabela-z

estatística

distribuição normal

cursos

escore-z

tabela z

Fundamentos práticos para padronização (z-score), leitura de probabilidades na tabela-z e aplicações comparativas.

Autor

Blog do Marcellini

Data de Publicação

24 de julho de 2025

← Índice da Distribuição Normal · ← Cursos de Estatística · ← Seção Estatística

1 🎓📊 Distribuição Normal — Parte 2

Nesta parte, focamos em padronização (escore-z), leitura da tabela-z e aplicações para comparar desempenhos, interpretar probabilidades e preparar o terreno para a inferência.

Nota

📌 Objetivos - Padronizar \(X\) via \(Z=\frac{X-\mu}{\sigma}\) e interpretar o escore-z. - Obter probabilidades pela tabela-z e por software (R/Python). - Comparar desempenhos em escalas distintas usando \(z\). - Preparar o uso de percentis e da normal inversa.

1.1 🧠 📖 Exercícios Resolvidos e Análise de Resultados

🧠 📖 Exercício 1 — Aplicando o Escore-z

Situação: Suponha que os escores de QI sigam uma distribuição normal com parâmetros:

\(\mu = 100\) (média)
\(\sigma = 16\) (desvio padrão)

Pergunta: Qual a probabilidade de uma pessoa ter QI superior a 136?

Instruções: 1. Calcule o escore-\(z\) correspondente a \(x=136\).
2. Use a tabela-z ou software para determinar \(P(Z>z)\).
3. Interprete o resultado: essa pontuação é comum ou rara?

💡 Dica:
\[ \boxed{\,z=\tfrac{x-\mu}{\sigma}\,}, \quad \boxed{\,P(Z>z)=1-P(Z<z)\,} \]

🧠 🔎 Resolução — Exercício 1

Distribuição: \(X \sim \mathcal N(100,\,16^2)\)

🧮 Passo 1 — Escore-z

\[ z = \frac{136-100}{16} = \frac{36}{16} = 2,25 \]

🧮 Passo 2 — Consulta na tabela-z

\[ P(Z<2{,}25) \approx 0{,}9878 \quad\Rightarrow\quad P(Z>2{,}25) = 1 - 0{,}9878 = 0{,}0122 \]

📌 Conclusão

Apenas cerca de \(\mathbf{1,22\%}\) da população tem QI superior a 136.
Ou seja, é um resultado raro, típico de indivíduos na cauda superior da distribuição.

1.2 📏 Comparando Desempenhos com Escore-z

Situação inicial:

Aluno A obteve nota 80 em uma prova com \(\mu=70,\; \sigma=5\).
Aluno B obteve nota 8 em uma prova com \(\mu=6,\; \sigma=1\).

Cálculo dos escores-\(z\):

\[ z_A = \frac{80-70}{5} = 2,0 \qquad z_B = \frac{8-6}{1} = 2,0 \]

📌 Conclusão:
Ambos os alunos tiveram desempenho 2 desvios-padrão acima da média de suas turmas.
Ou seja, o desempenho relativo foi equivalente.

🧠 📖 Exercício 2 — Comparando Desempenhos com Escore-z

Situação:

Aluno A obteve nota 65 em uma prova com \(\mu=60,\; \sigma=4\).
Aluno B obteve nota 7 em uma prova com \(\mu=5,5,\; \sigma=1\).

Tarefa: 1. Calcule o escore-\(z\) para os dois alunos.
2. Compare os valores.
3. Interprete: qual deles se destacou mais em relação à média da sua turma?

💡 Dica: quanto maior o valor de \(z\), melhor o desempenho relativo.

🧠 🔎 Resolução — Exercício 2

Aluno A:

\[ z_A = \frac{65-60}{4} = \frac{5}{4} = 1,25 \]

Aluno B:

\[ z_B = \frac{7-5{,}5}{1} = \frac{1{,}5}{1} = 1,5 \]

📌 Conclusão:
O Aluno B obteve \(z_B=1,5\), maior que o \(z_A=1,25\).
Portanto, o Aluno B apresentou melhor desempenho relativo em relação à sua turma.

✏️📄 Resumo — Distribuição Normal e Escore-z

Distribuição Normal:

\[ \boxed{\, f(x)=\tfrac{1}{\sqrt{2 \pi \sigma^2}} \, e^{-\tfrac{(x-\mu)^2}{2 \sigma^2}} \,} \]

Distribuição Normal Padrão (\(\mu=0,\; \sigma=1\)):

\[ \boxed{\, f(z)=\tfrac{1}{\sqrt{2 \pi}} \, e^{-z^2/2} \,} \]

Escore-z (padronização):

\[ \boxed{\, z=\tfrac{x-\mu}{\sigma} \,} \]

Valor original a partir de \(z\):

\[ \boxed{\, x=\mu+z\sigma \,} \]

Regra Empírica (68–95–99,7):
- \(68\%\): entre \(\mu \pm 1\sigma\)
- \(95\%\): entre \(\mu \pm 2\sigma\)
- \(99{,}7\%\): entre \(\mu \pm 3\sigma\)

1.3 📊 Tabela-z — Distribuição Normal Padrão

Como usar a tabela-z: - A linha indica a parte inteira e a 1ª casa decimal do escore-\(z\).
- A coluna indica a 2ª casa decimal.
- A interseção fornece \(P(Z<z)\), isto é, a probabilidade acumulada até \(z\).

z	0.00	0.01	0.02	0.03	0.04	0.05
1.2	0.8849	0.8869	0.8888	0.8907	0.8925	0.8944

🧠 Exemplo:
Para \(z=1,25\), usamos a linha 1.2 e a coluna 0.05, obtendo:
\[ P(Z<1{,}25)=0{,}8944 \]

1.4 📊 Tabela-z Acumulada — Normal Padrão \([P(Z<z)]\)

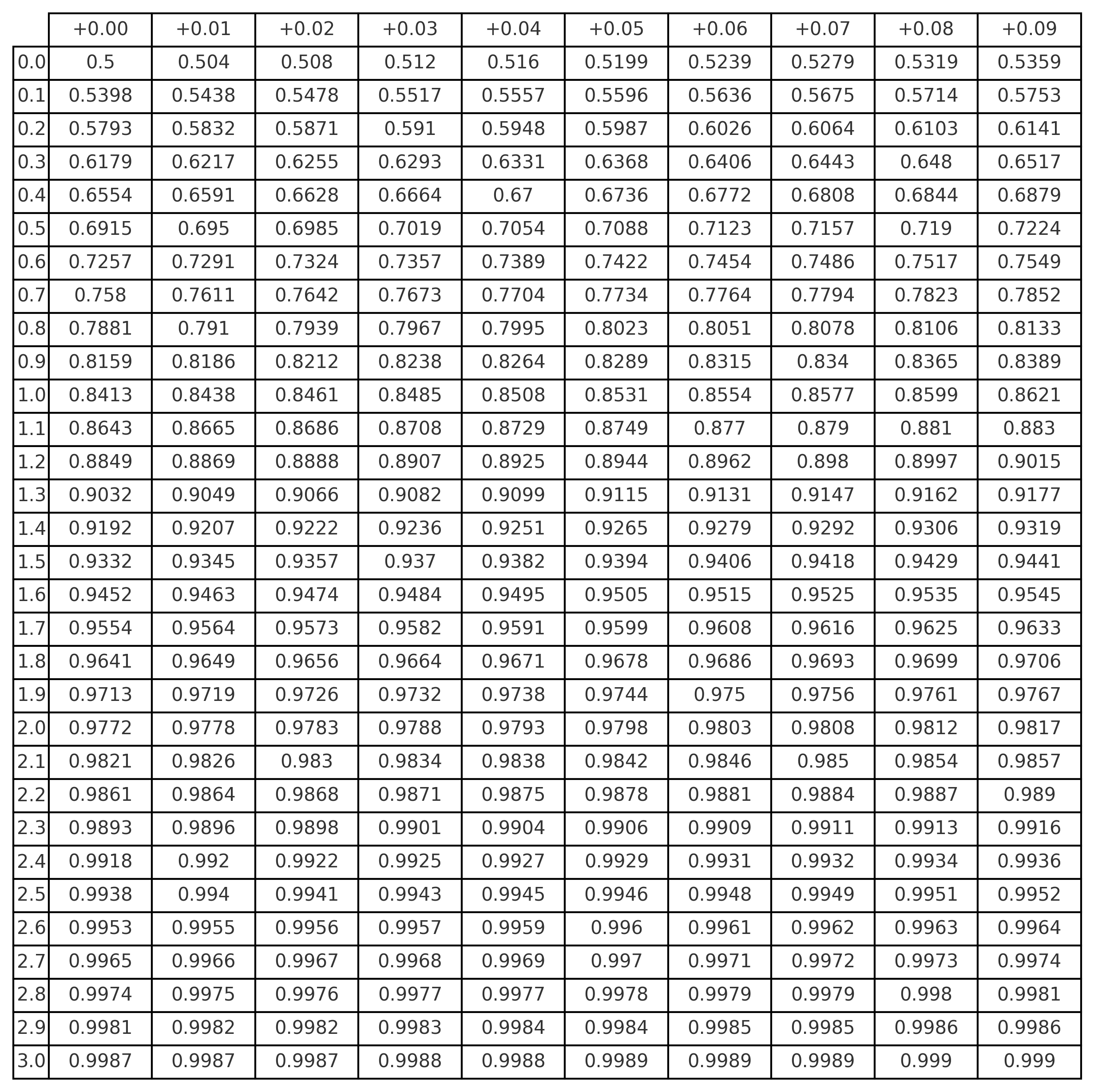
Tabela-z acumulada com valores de probabilidade até z.

Fonte: gerada com scipy.stats.norm.cdf para valores de \(z\) entre 0,00 e 3,09.

💻 Atividades Práticas — Excel e R

Objetivo: aplicar os conceitos de distribuição normal e escore-\(z\) em ambiente computacional.

No Excel:

=NORM.DIST(120;100;16;VERDADEIRO) → calcula \(P(X<120)\).
=NORM.INV(0,90;100;16) → retorna o valor correspondente ao percentil 90.
Gere uma tabela com valores de \(x\), calcule os escores-\(z\) e destaque quem está acima da média.

No R:

pnorm(120, mean=100, sd=16) → retorna \(P(X<120)\).
qnorm(0.90, mean=100, sd=16) → retorna o valor do percentil 90.
z <- (x - mean)/sd → calcula escore-\(z\) de um vetor.

💡 Sugestão: compare alunos de diferentes turmas (com diferentes médias e desvios), usando o escore-\(z\).

🧠 📈 Desafio com Gráfico — Distribuição Normal

Situação:
O tempo de atendimento (em minutos) em um serviço segue \(X \sim \mathcal N(50, 10^2)\).

Tarefa:

Marque no gráfico as regiões correspondentes a:
- \(P(40<X<60)\)
- \(P(X>70)\)
Calcule os escores-\(z\) correspondentes a 40, 60 e 70.
Use Excel ou R para calcular as probabilidades dessas regiões.
Interprete: são tempos de atendimento comuns ou raros?

💡 Dica: use a regra empírica e a simetria da curva como apoio visual.

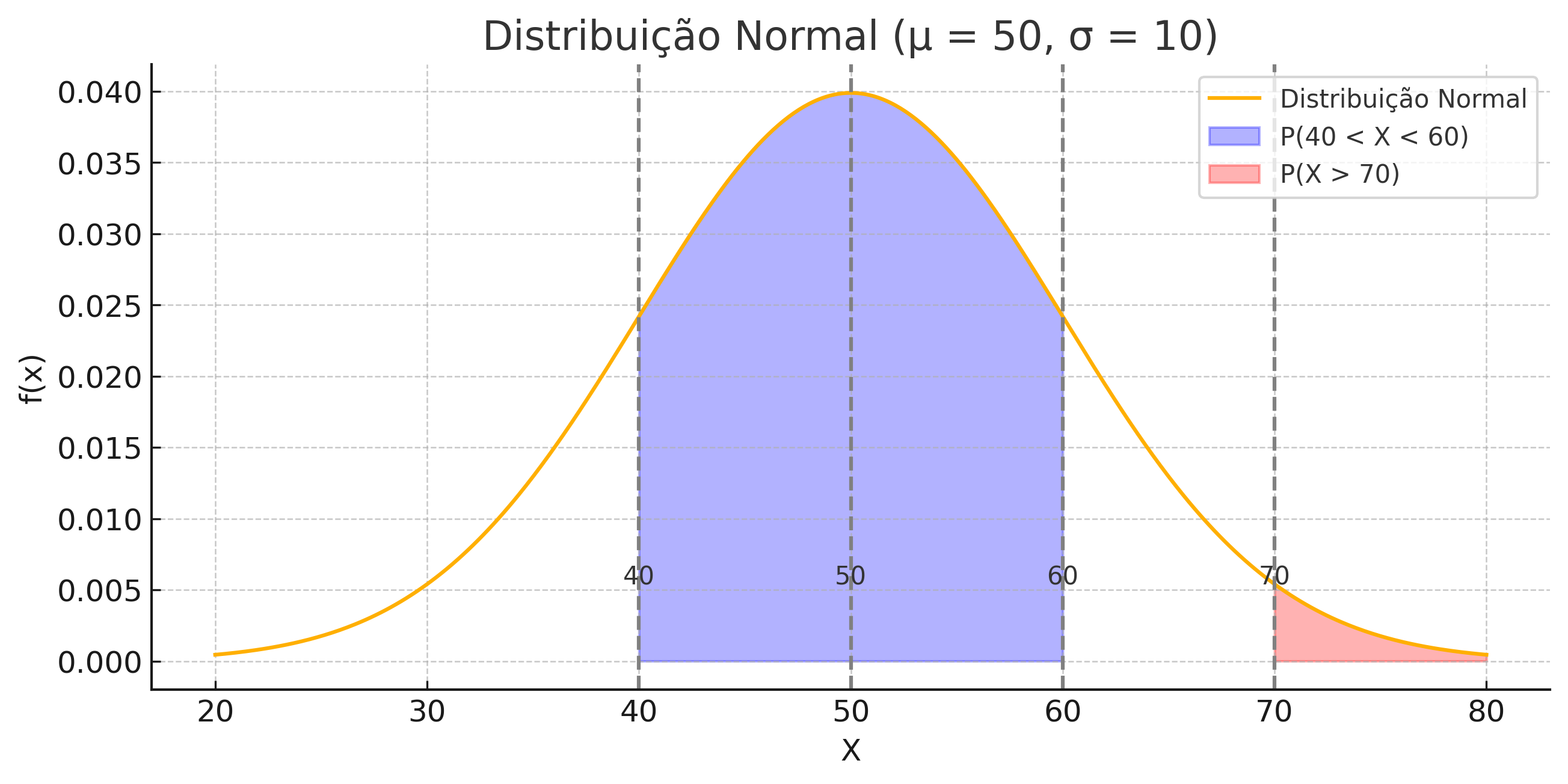
Gráfico da distribuição normal N(50,10²) com áreas destacadas entre 40–60 e acima de 70.

A curva mostra a distribuição \(X \sim \mathcal N(50, 10^2)\).
As áreas coloridas representam: Azul: \(P(40<X<60)\), Vermelho: \(P(X>70)\).

🧠 🔎 Gabarito — Desafio com Gráfico

Distribuição: \(X \sim \mathcal N(50, 10^2)\)

Escore-\(z\): \[ z_{40} = \frac{40-50}{10} = -1, \quad z_{60} = \frac{60-50}{10} = 1, \quad z_{70} = \frac{70-50}{10} = 2 \]
Probabilidades:

\(P(40<X<60) = P(-1<Z<1) \approx 0{,}6826\)
\(P(X>70) = P(Z>2) = 1-P(Z<2) \approx 0{,}0228\)

📌 Interpretação:
- Cerca de \(\mathbf{68,26\%}\) dos atendimentos duram entre 40 e 60 minutos.
- Apenas \(\mathbf{2,28\%}\) dos atendimentos duram mais de 70 minutos → são raros.

💻 Gabarito — Usando Excel e R

Distribuição: \(X \sim \mathcal N(50, 10^2)\)

No Excel:

\(P(40<X<60)\):
=NORM.DIST(60;50;10;VERDADEIRO) - NORM.DIST(40;50;10;VERDADEIRO)
→ \(\approx 0{,}6826\)
\(P(X>70)\):
=1 - NORM.DIST(70;50;10;VERDADEIRO)
→ \(\approx 0{,}0228\)

No R:

\(P(40<X<60):\) pnorm(60, mean=50, sd=10) - pnorm(40, mean=50, \(\mathrm{sd}=10\) )
\(P(X>70): 1-\operatorname{pnorm}(70\), mean \(=50, \mathrm{sd}=10)\)

Resultados aproximados: \(P(40<X<60) \approx 68,26 \%, P(X>70) \approx 2,28 \%\).

1.5 Importância da Distribuição Normal na Estatística

A distribuição normal é mais do que uma curva bonita: ela é fundamental na estatística aplicada.
Muitos métodos inferenciais dependem da normalidade:
Testes de hipóteses (teste \(z\), teste \(t\))
Construção de intervalos de confiança
Análises de regressão linear
Aproximações para distribuições amostrais
Conhecer a distribuição normal é o primeiro passo para entender a inferência estatística!

📌 Observação: A distribuição normal conecta a análise descritiva à análise inferencial - o próximo grande passo na estatística!

1.6 📌 Conclusão da Parte 2: Escore-z e Tabela Z

A Parte 2 do curso aprofundou o uso prático da distribuiçāo normal e do escore-\(z\):

Comparação de desempenhos
Interpretação gráfica e computacional de probabilidades
Fundamentação para estudos futuros em inferência estatística

2 📚 Referências

Importante

Schmuller, Joseph. Statistical Analysis with Excel® For Dummies®, 5ª ed. Wiley, 2016.
Schmuller, Joseph. Análise Estatística com R Para Leigos, 2ª ed. Alta Books, 2021.
Levine, D. M.; Stephan, D.; Szabat, K. A. Statistics for Managers Using Microsoft Excel, 8ª ed. Pearson, 2017.
Morettin, L. G. Estatística Básica: Probabilidade e Inferência, 7ª ed. Pearson, 2017.
Morettin, P. A.; Bussab, W. O. Estatística Básica, 10ª ed. SaraivaUni, 2023.

3 🔗 Acesso Rápido às Partes do Curso

🎯 Parte 1: Introdução à Distribuição Normal
🎯 Parte 2: Escore-z e Tabela-z (👉 você está aqui!)
🎯 Parte 3: Gráficos, TCL e Normalidade Aproximada