🎓📊 Distribuição Normal — Parte 3: Gráficos, TCL e Normalidade Aproximada

estatística
distribuição normal
cursos
teorema central do limite
lei dos grandes números
normalidade aproximada
Fundamentos visuais e teóricos: histogramas, Q-Q plots, Lei dos Grandes Números e Teorema Central do Limite como base para a normalidade aproximada.
Autor

Blog do Marcellini

Data de Publicação

24 de julho de 2025

· ← Sumário do Curso · ← Cursos de Estatística · ← Seção de Estatística

Curva da distribuição normal (Gauss), simétrica em torno da média.

1 🎓📊 Distribuição Normal — Parte 3

Nesta parte, abordaremos a avaliação da normalidade de dados reais, tanto de forma visual (histogramas, Q-Q plots) quanto teórica (Lei dos Grandes Números e Teorema Central do Limite). A normalidade aproximada é a ponte entre análise descritiva e inferência estatística.

Nota

📌 Objetivos deste post

  • Identificar variáveis que seguem aproximadamente a distribuição normal.
  • Reconhecer que a normalidade é uma suposição-chave para muitos métodos estatísticos.
  • Utilizar gráficos (histogramas, Q-Q plots) para avaliar a normalidade dos dados.
  • Interpretar de forma prática e aplicada os resultados da análise de normalidade.

1.1 🧠 Complementos — Entendendo a Normalidade no Mundo Real

Nesta parte, com base em Levine et al., Statistics for Managers Using Microsoft Excel, exploramos quando e como a distribuição normal pode ser utilizada como uma aproximação válida em contextos reais.

🎯 Objetivos:

  • Compreender em que condições variáveis podem ser tratadas como aproximadamente normais.
  • Reconhecer a importância da normalidade para métodos de inferência estatística.
  • Utilizar critérios práticos e gráficos para avaliar a normalidade dos dados.

🧠 Vamos aprofundar nossa compreensão!

1.2 📈 ❓ O que é uma Distribuição Aproximadamente Normal?

Chamamos de distribuições aproximadamente normais aquelas variáveis que, mesmo sem seguir exatamente a curva normal, apresentam características suficientes para que métodos estatísticos baseados na normalidade sejam aplicados.

👉 Características principais:

  • Forma de sino (bell-shaped) e simetria em torno da média.
  • Maior concentração de observações próximas da média, com poucas ocorrências extremas.
  • A maioria dos valores concentrada dentro de 1 a 2 desvios-padrão da média.

❗ Observações importantes:

  • Nem toda variável precisa ser perfeitamente normal para que possamos aplicar testes estatísticos.
  • Pequenas assimetrias ou irregularidades geralmente são toleráveis.
  • Muitas distribuições reais não são exatamente normais, mas sim aproximadamente normais.

📌 Exemplos típicos:

  • Altura de adultos.
  • Tempos de atendimento em serviços.
  • Processos industriais sob controle estatístico.
Nota📈 📝 Exemplos de Distribuições: Normais e Não Normais

✅ Variáveis aproximadamente normais:

  • Altura de adultos de uma mesma população.
  • Tempo de atendimento em serviços padronizados.
  • Erros de medição sob condições controladas.

❌ Variáveis não normalmente distribuídas:

  • Renda de famílias (tendência à direita — assimetria positiva).
  • Número de filhos por família (discreta, assimétrica).
  • Tempo de vida de equipamentos eletrônicos (cauda longa à direita).

📌 Observação:
Algumas variáveis podem se aproximar da normalidade após transformações, como logaritmo ou raiz quadrada.

Nota📈 📝 Exemplos Reais de Normalidade Aproximada

Exemplos de variáveis com distribuição aproximadamente normal:

  • Alturas de estudantes universitários.
  • Tempos de atendimento telefônico em call centers padronizados.
  • Pesos de recém-nascidos em hospitais.
  • Notas em testes padronizados (ex.: exames de proficiência).
  • Erros de medição em experimentos físicos controlados.
  • Idades de aposentadoria em grandes populações.

❗ Importante:
Mesmo que a distribuição real não seja perfeitamente normal, uma aproximação normal geralmente é suficiente para aplicações práticas e inferências estatísticas.

1.3 📈 ❓ O que é um Gráfico Q-Q Plot?

📊 O Q-Q Plot (Quantile–Quantile Plot) é um gráfico usado para comparar a distribuição de dados amostrais com uma distribuição teórica — geralmente a normal.

🎯 Objetivos:

  • Avaliar se os dados seguem aproximadamente uma distribuição normal.
  • Identificar desvios relevantes, como assimetrias ou caudas pesadas.

🔎 Como interpretar:

  • Se os pontos se alinham próximos a uma linha reta diagonal, os dados são aproximadamente normais.
  • Desvios sistemáticos (curvaturas ou caudas afastadas) indicam falta de normalidade.

📌 Observação:
O Q-Q Plot é especialmente útil em amostras grandes, pois pequenas imperfeições são esperadas e não comprometem a interpretação global.

Nota📈 📝 Exemplo Visual — Histograma de uma Distribuição Normal

👉 Situação:

  • Amostra de 200 alturas de adultos.
  • Média observada: \(170\) cm.
  • Desvio padrão observado: \(8\) cm.

📈 Gráfico:

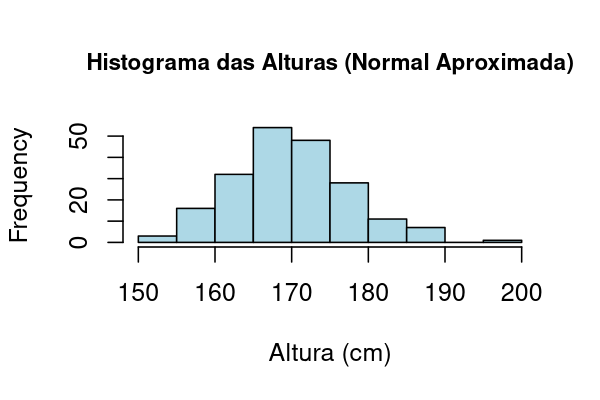
Histograma de 200 alturas de adultos, com média 170 e desvio padrão 8, mostrando formato de sino.

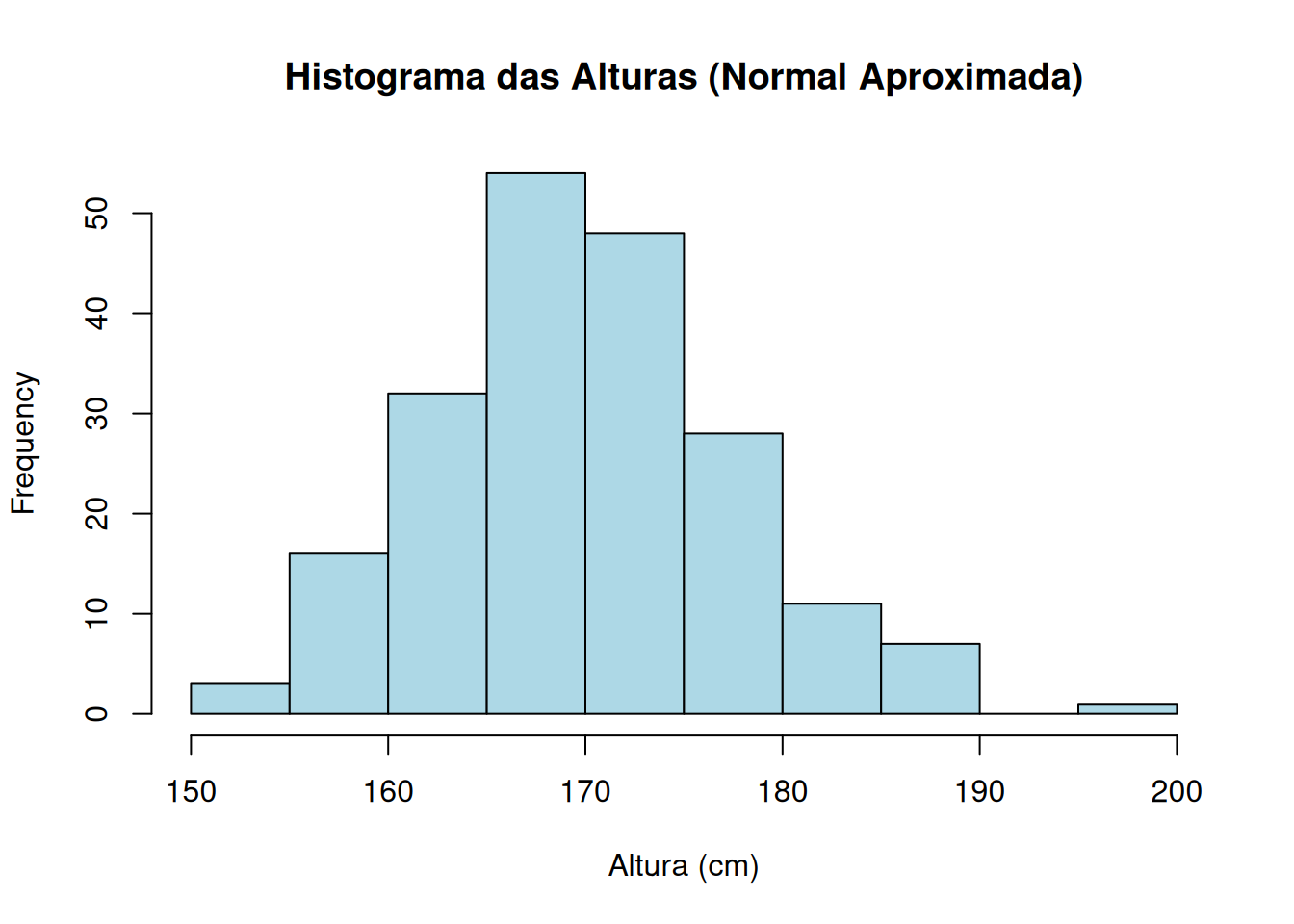
Gráfico gerado no R a partir de 200 observações simuladas de \(X \sim \mathcal N(170,\,8^2)\).

🔎 Interpretação:
O histograma apresenta formato de sino, simétrico em torno da média.
Pequenas variações são esperadas, mas a aproximação à distribuição normal é muito boa.

Nota📈 📝 Exemplo Visual — Gráfico Q-Q Plot (Levine)

👉 Situação:
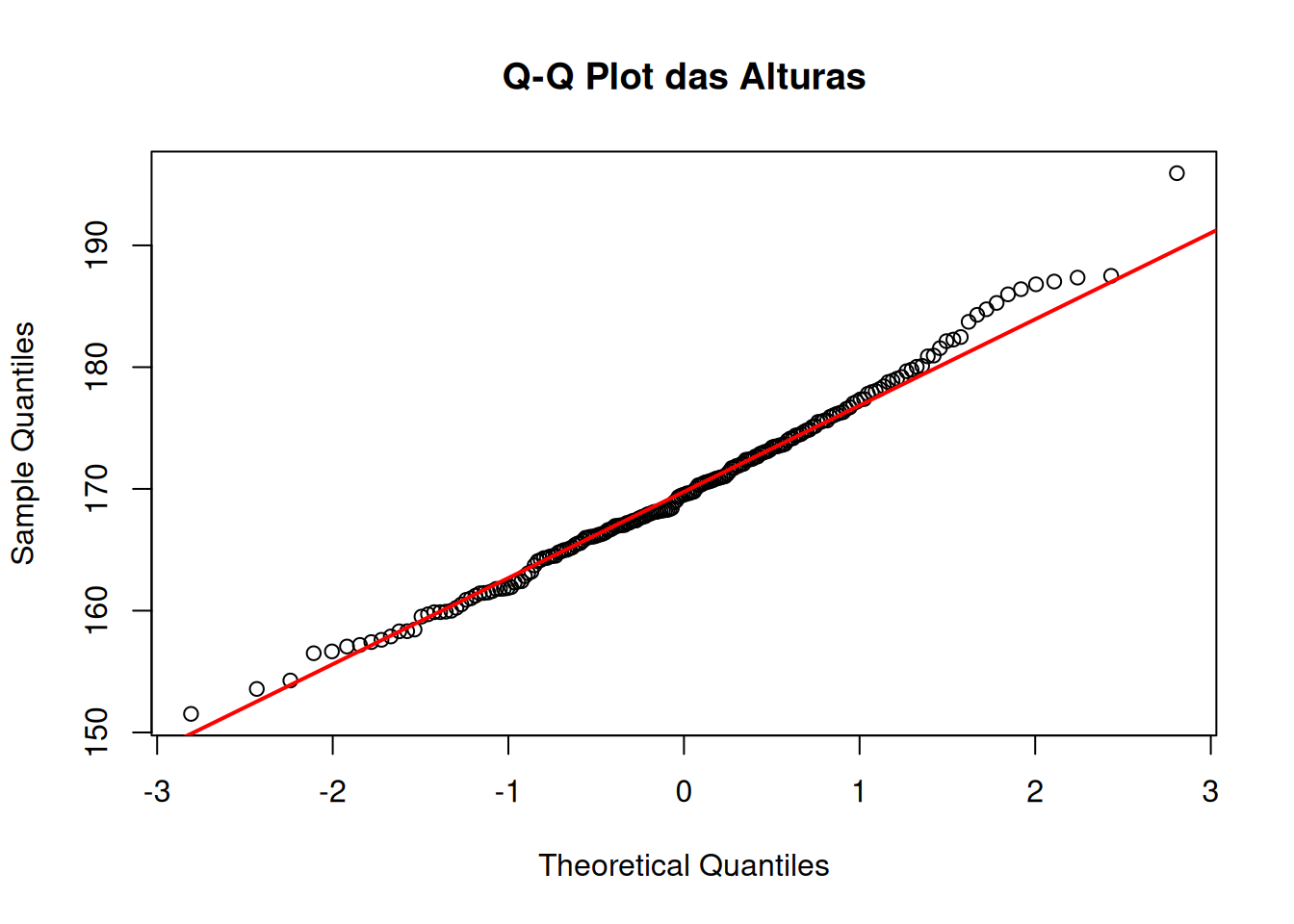
A mesma amostra de 200 alturas de adultos (\(\mu=170,\; \sigma=8\)) foi utilizada para construir o Q-Q plot.

📈 Gráfico:

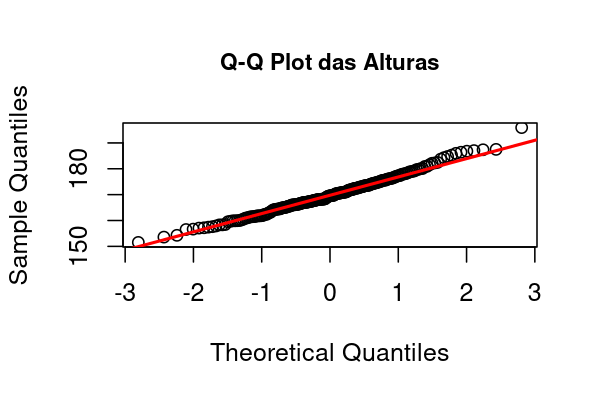
Q-Q Plot de 200 alturas simuladas de uma distribuição normal com média 170 e desvio padrão 8.

Gráfico gerado no R com 200 observações simuladas de \(X \sim \mathcal N(170,\,8^2)\).

🔎 Interpretação:

  • Quando os pontos se alinham aproximadamente sobre a linha reta, concluímos que a distribuição é aproximadamente normal.
  • Pequenas flutuações são esperadas em amostras reais e não invalidam a análise.

🎯 Objetivo: Gerar uma amostra de alturas e visualizar o histograma e o Q-Q plot diretamente no RStudio.

# Gerar a amostra de alturas
set.seed(123) # Garante reprodutibilidade
alturas <- rnorm(200, mean = 170, sd = 8)

# Exibir o Histograma
hist(alturas,
breaks = 15,
main = "Histograma das Alturas (Normal Aproximada)",
xlab = "Altura (cm)",
col = "lightblue",
border = "black")

# Exibir o Q-Q Plot
qqnorm(alturas,
main = "Q-Q Plot das Alturas")
qqline(alturas, col = "red", lwd = 2)

📌 Observação: O código gera os gráficos diretamente na tela do RStudio.

1.4 🧭 Passo a Passo para Gerar os Gráficos no RStudio

🎯 Objetivo: Construir o Histograma e o Q-Q Plot da amostra de alturas usando o RStudio.

👉 (1) Gerar a amostra:

  • Use rnorm () para criar dados aleatórios com distribuição normal.

👉 (2) Construir o Histograma:

  • Use a função hist() para visualizar a distribuição dos dados.

👉 (3) Construir o Q-Q Plot:

  • Use qqnorm() para criar o gráfico.

  • Adicione a linha de referência com qqline().

❗ Importante: Visualize e interprete os gráficos na tela antes de aplicar métodos estatísticos!

Dica🔍 Por que visualizar os gráficos antes da análise?

Antes de aplicar qualquer técnica estatística, é essencial explorar visualmente os dados. Gráficos como histogramas e Q-Q plots ajudam a verificar suposições fundamentais, como a normalidade, a presença de outliers e a simetria da distribuição.

Aplicar testes estatísticos sem essa verificação prévia pode levar a conclusões equivocadas ou estatisticamente inválidas. A visualização gráfica permite detectar padrões, desvios e anomalias que os números sozinhos não revelam — sendo, portanto, uma etapa crítica no processo de análise de dados.

NotaAtividade 1: Gerando e Interpretando Novos Gráficos no RStudio

🎯 Objetivo: Aplicar o que foi aprendido para gerar novos gráficos no RStudio.

🧠 📝 Tarefa:

👉 (1) Gere uma nova amostra de 200 observações normalmente distribuídas com:

  • Média \((\mu)=160\)

  • Desvio padrão \((\sigma)=5\)

👉 (2) Construa:

  • Um Histograma das alturas geradas.

  • Um Q-Q Plot correspondente.

👉 (3) Compare visualmente:

  • A forma do novo histograma.

  • O alinhamento dos pontos no Q-Q plot.

💡 Dica: Use as mesmas funções: rnorm(), hist(), qqnorm(), qqline().

🧑‍💻 Código no R :

# Gerar nova amostra
set.seed(456) # Nova semente para variar os dados
alturas_novas <- rnorm(200, mean = 160, sd = 5)

# Histograma
hist(alturas_novas,
breaks = 15,
main = "Histograma das Alturas (Nova Amostra)",
xlab = "Altura (cm)",
col = "lightgreen",
border = "black")

# Q-Q Plot
qqnorm(alturas_novas,
main = "Q-Q Plot das Alturas (Nova Amostra)")
qqline(alturas_novas, col = "blue", lwd = 2)

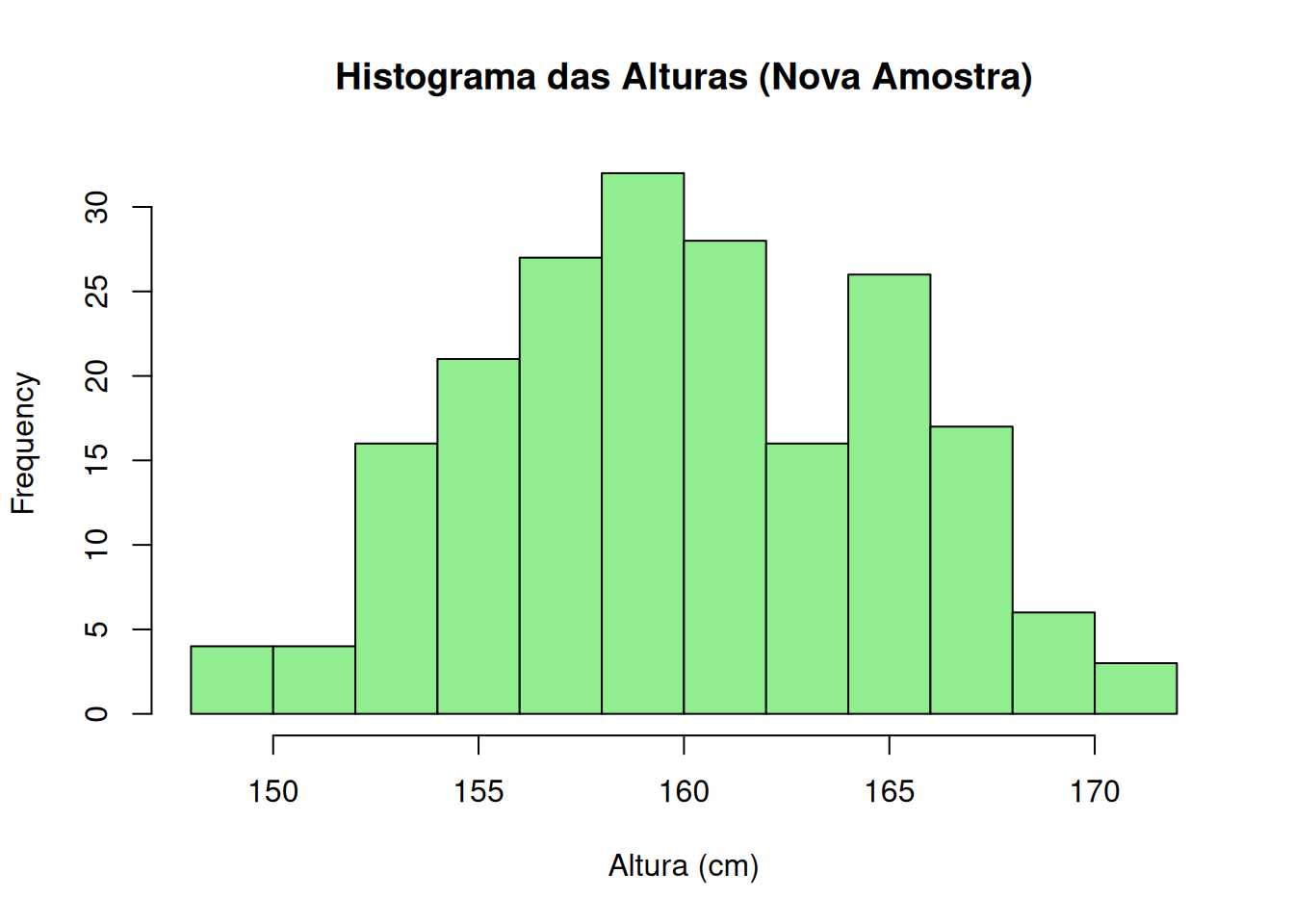
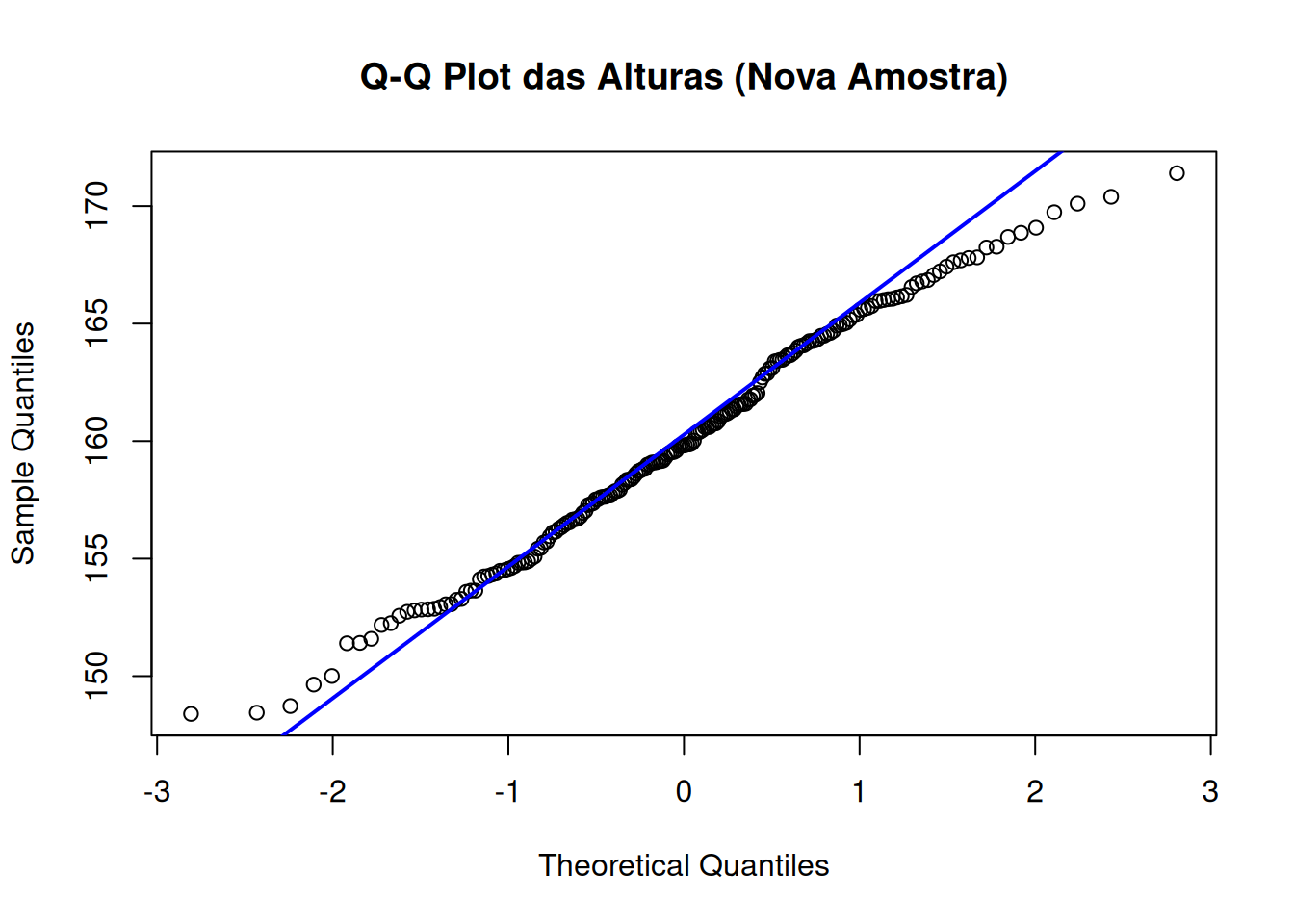
📌 Interpretação: Os novos dados também seguem aproximadamente uma distribuição normal.

1.5 🧭 Passo a Passo para Gerar Gráficos no Excel

🎯 Objetivo: Construir o Histograma e o Q-Q Plot da amostra de alturas usando o Excel.

📈 Histograma no Excel:

  1. Insira os dados da amostra em uma coluna.

  2. Selecione os dados.

  3. Vá em Inserir \(\rightarrow\) Gráficos Estatísticos \(\rightarrow\) Histograma.

  4. Ajuste o número de intervalos (bins) conforme necessário.

📈 Q-Q Plot no Excel:

  1. Ordene os dados da amostra (crescente).

  2. Calcule a posição teórica dos quantis: =NORM.INV((Linha - 0,5)/Total, Média, Desvio_padrão).

  3. Construa um gráfico de dispersão (XY Scatter) dos dados amostrais vs. quantis teóricos.

  4. Adicione uma linha de tendência linear para referência.

📌 Observação: O Q-Q Plot é manual no Excel, mas fácil de construir!

1.6 🧠 Lei dos Grandes Números (LGN)

  • Amostras grandes tendem a refletir a verdadeira média populacional.

  • A variabilidade diminui conforme aumentamos o tamanho da amostra.

📌 Resumo: A LGN assegura que médias amostrais se aproximam da média populacional.

1.7 🧠 Teorema Central do Limite (TCL)

  • A média de amostras grandes tende a seguir uma distribuição normal.

  • Independentemente da distribuição original!

Conclusão: O TCL é a base teórica para o uso da distribuição normal na prática.

1.8 🧠 Variabilidade e Forma da Curva Normal

  • \(\sigma\) pequeno \(\rightarrow\) curva mais estreita.

  • \(\sigma\) grande \(\rightarrow\) curva mais achatada.

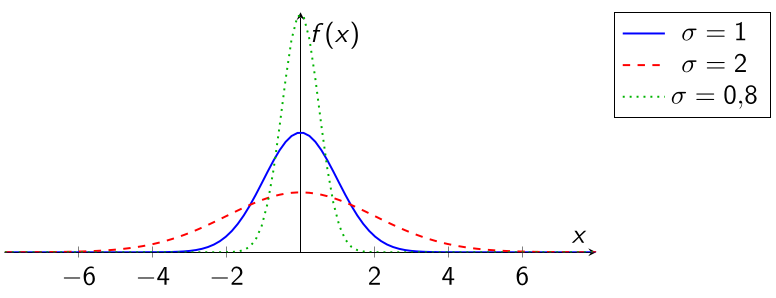
Variabilidade e Forma da Curva Normal
Nota🧠 📖 Teste Rápido: Verdadeiro ou Falso?

  1. Uma curva normal com maior \(\sigma\) é mais estreita? (V ou F)

  2. Pela LGN, amostras pequenas já refletem a média real? (V ou F)

  3. O TCL explica a prevalência da normalidade? (V ou F)

  1. Uma curva normal com maior \(\sigma\) é mais estreita? (F)

  2. Pela LGN, amostras pequenas já refletem a média real? (F)

  3. O TCL explica a prevalência da normalidade? (V)

📌 Observação: Compreender a normalidade é essencial para aplicar corretamente testes estatísticos e tomar decisões baseadas em dados!

1.9 📌 Conclusão da Parte 3: Gráficos, TCL e Normalidade Aproximada

Nesta última parte do curso, você aprendeu:

  • A identificar variáveis que seguem uma distribuição aproximadamente normal.

  • A reconhecer que a normalidade é uma suposição chave para muitos métodos estatísticos.

  • A utilizar gráficos como histogramas e diagramas de probabilidade normal (Q-Q plots) para avaliar a normalidade dos dados.

  • A interpretar os resultados da análise de normalidade de forma prática e aplicada.

2 📚 Referências

  • Schmuller, Joseph. Statistical Analysis with Excel® For Dummies®, 5ª ed. Wiley, 2016.
  • Schmuller, Joseph. Análise Estatística com R Para Leigos, 2ª ed. Alta Books, 2021.
  • Levine, D. M.; Stephan, D.; Szabat, K. A. Statistics for Managers Using Microsoft Excel, 8ª ed. Pearson, 2017.
  • Morettin, L. G. Estatística Básica: Probabilidade e Inferência, 7ª ed. Pearson, 2017.
  • Morettin, P. A.; Bussab, W. O. Estatística Básica, 10ª ed. SaraivaUni, 2023.

3 🔗 Acesso Rápido às Partes do Curso

🎯 Parte 1: Introdução à Distribuição Normal
🎯 Parte 2: Escore-z e Tabela Z
🎯 Parte 3: Gráficos, TCL e Normalidade Aproximada (👉 você está aqui!)

· ← Sumário do Curso · ← Cursos de Estatística · ← Seção de Estatística

· 🔝 Topo

Blog do Marcellini — Explorando a Estatística com Rigor e Beleza.

Nota

📌 Criado por Blog do Marcellini com ❤️ e código.