📘 Módulo 1.3: Intervalos e Inequações

Definição de ordem em R, intervalos e inequações lineares e quadráticas, com exemplos, teoremas e diagramas.

← Voltar ao Sumário do Curso 🎓🧮 · ← Cursos de Matemática · ← Seção de Matemática

🎯 Post Anterior: 👉 1.2 Conjuntos Numéricos (Aprofundamento)

---

1 Ordem em \(\mathbb{R}\)

Nota📖 Definição — Ordem Estrita

Sejam \(a,b \in \mathbb{R}\): 1. \(a < b \iff b-a > 0\); 2. \(a > b \iff a-b > 0\).

1.1 Exemplos

• \(3<7\), pois \(7-3=4>0\).

• \(-5<-2\), pois \(-2-(-5)=3>0\).

Diagrama genérico:

---

2 Desigualdades Não-Estritas

Nota📖 Definição — Ordem Não-Estrita

Sejam \(a,b \in \mathbb{R}\):

1. \(a \leqslant b \iff (a<b) \text{ ou } (a=b)\);
2. \(a \geqslant b \iff (a>b) \text{ ou } (a=b)\).

• \(a<b\) e \(a>b\): desigualdades estritas.
  
• \(a\leqslant b\) e \(a\geqslant b\): desigualdades não-estritas.

---

3 Teoremas Fundamentais da Ordem

Importante📐 Teorema 1 — Sinais

1. \(a>0 \iff a\) é positivo.
   
2. \(a<0 \iff a\) é negativo.

Importante📐 Teorema 2 — Transitividade

Se \(a<b\) e \(b<c\), então \(a<c\).

Importante📐 Teorema 3 — Adição e Multiplicação

1. Se \(a<b\), então \(a+c<b+c\).
   
2. Se \(a<b\) e \(c>0\), então \(ac<bc\).
   
3. Se \(a<b\) e \(c<0\), então \(ac>bc\).

Importante📐 Teorema 4 — Soma de Desigualdades

Se \(a<b\) e \(c<d\), então \(a+c<b+d\).

---

4 Cadeias de Desigualdades

Um número \(x\) está entre \(a\) e \(b\) se \(a<x<b\).
Exemplo: \(2<x<5\).

Outras formas:
- \(a \leqslant x \leqslant b\) → intervalo fechado;
- \(a \leqslant x < b\), \(a < x \leqslant b\) → intervalos semiabertos.

---

5 Intervalos

5.1 Intervalo aberto

\[(a,b) = \{x\in\mathbb{R}\mid a<x<b\}\]

5.2 Intervalo fechado

\[[a,b] = \{x\in\mathbb{R}\mid a\leqslant x\leqslant b\}\]

5.3 Semiabertos

• \((a,b] = \{x \mid a<x\leqslant b\}\)
  

• \([a,b) = \{x \mid a\leqslant x<b\}\)

5.4 Infinitos

• \((a,+\infty) = \{x \mid x>a\}\)
  

• \((-\infty,b) = \{x \mid x<b\}\)
  

• \([a,+\infty) = \{x \mid x\geqslant a\}\)

• \((-\infty,b] = \{x \mid x\leqslant b\}\)

• \((-\infty,+\infty)=\mathbb{R}\)

---

6 Inequações Lineares

Forma geral (com \(a \neq 0\)):

\[ \boxed{\, ax+b < c \,} \]

\[ \boxed{\, ax+b \leqslant c \,} \]

\[ \boxed{\, ax+b > c \,} \]

\[ \boxed{\, ax+b \geqslant c \,} \]

---

📌 Observação importante:
- Se \(a=0\), a inequação se reduz a uma afirmação constante (\(b<c\), \(b\leqslant c\), etc.), sem variável.
- Se \(a\neq 0\), podemos isolar \(x\):

• Para \(a>0\), a ordem é preservada.
  
• Para \(a<0\), a desigualdade inverte o sinal.

Nota🧮 Exemplos — Inequações Lineares

6.1 Casos com \(a>0\)

1. \(2x-3<5 \;\;\Rightarrow\;\; x<4\)
   Solução: \((-\infty,4)\).

2. \(3x+1\leqslant 7 \;\;\Rightarrow\;\; x\leqslant 2\)
   Solução: \((-\infty,2]\).

3. \(5x-4>11 \;\;\Rightarrow\;\; x>3\)
   Solução: \((3,+\infty)\).

4. \(4x+2\geqslant 10 \;\;\Rightarrow\;\; x\geqslant 2\)
   Solução: \([2,+\infty)\).

---

6.2 Casos com \(a<0\)

5. \(-2x+3<7 \;\;\Rightarrow\;\; x>-2\)
   Solução: \((-2,+\infty)\).

6. \(-3x+1\leqslant -8 \;\;\Rightarrow\;\; x\geqslant 3\)
   Solução: \([3,+\infty)\).

7. \(-4x+5>1 \;\;\Rightarrow\;\; x<1\)
   Solução: \((-\infty,1)\).

8. \(-x-2\geqslant 5 \;\;\Rightarrow\;\; x\leqslant -7\)
   Solução: \((-\infty,-7]\).

---

📌 Resumo importante:
- Se \(a>0\), a desigualdade mantém o sentido.
- Se \(a<0\), a desigualdade inverte o sentido.

Nota🧮 Exemplos resolvidos em detalhes

• Exemplo 1: \(2x-3<5\) (coeficiente \(a>0\))

\[ \begin{aligned} 2x-3 &< 5 && \text{(dado)}\\ 2x &< 5+3 = 8 && \text{(somar 3 dos dois lados)}\\ x &< \frac{8}{2} = 4 && \text{(dividir por 2>0, preserva o sinal)} \end{aligned} \]

✅ Solução (intervalo): \((-\infty,4)\).
📌 Checagem: \(x=3 \Rightarrow 3<5\) (verdadeiro); \(x=4 \Rightarrow 5\not<5\) (falso).

---

• Exemplo 5: \(-2x+3<7\) (coeficiente \(a<0\))

\[ \begin{aligned} -2x+3 &< 7 && \text{(dado)}\\ -2x &< 7-3 = 4 && \text{(subtrair 3 dos dois lados)}\\ x &> \frac{4}{-2} = -2 && \text{(dividir por -2<0, \textbf{inverte} o sinal)} \end{aligned} \]

✅ Solução (intervalo): \((-2,+\infty)\).
📌 Checagem: \(x=0 \Rightarrow 3<7\) (verdadeiro); \(x=-2 \Rightarrow 7\not<7\) (falso).

---

Resumo didático:
- Somar/subtrair: mantém o sentido.
- Multiplicar/dividir por número positivo: mantém o sentido.
- Multiplicar/dividir por número negativo: inverte o sentido.

---

7 Inequações Quadráticas

Forma geral (com \(a \neq 0\)):

\[ \boxed{ax^2 +bx + c < 0} \]

\[ \boxed{ax^2 +bx + c > 0} \]

\[ \boxed{ax^2 +bx + c \leqslant 0} \]

\[ \boxed{ax^2 +bx + c \geqslant 0} \]

---

Resolver analisando a parábola \(y=ax^2+bx+c\).

📌 Exemplo 1: \(x^2-5x+6>0\)
- Raízes: \(x=2,3\)
- Parábola abre para cima.
- Sinal positivo fora de \((2,3)\).
- Solução: \((-\infty,2)\cup(3,+\infty)\).

Diagrama na reta real:

Gráfico da parábola:

---

📌 Exemplo 1: \(x^2-5x+6>0\)

Nota🧮 Resolução detalhada

1. Identificação: trata-se de uma inequação quadrática com \(a=1>0\), \(b=-5\), \(c=6\).

2. Equação associada:
   \[ x^2 - 5x + 6 = 0 \]

3. Discriminante (Δ):
   \[ \Delta = b^2 - 4ac = (-5)^2 - 4\cdot 1 \cdot 6 = 25 - 24 = 1 \]

4. Raízes reais:
   \[ x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{5 \pm 1}{2} \] Logo, \(x_1=2\) e \(x_2=3\).

5. Esboço da parábola: como \(a=1>0\), a parábola é côncava para cima.

6. Sinal da parábola:

   • Para \(x<2\), a parábola está acima do eixo (\(f(x)>0\)).
     
   • Para \(2<x<3\), a parábola está abaixo do eixo (\(f(x)<0\)).
     
   • Para \(x>3\), a parábola volta a ficar acima do eixo (\(f(x)>0\)).

7. Conclusão (solução da inequação \(f(x)>0\)):
   \[ x \in (-\infty,2)\cup(3,+\infty) \]

Diagrama na reta real:

Gráfico da parábola e estudo do sinal:

---

📌 Exemplo 2: \(-x^2+4x-3 \geqslant 0\)

Nota🧮 Resolução detalhada

1. Identificação: inequação quadrática com \(a=-1<0\), \(b=4\), \(c=-3\).

2. Equação associada:
   \[ -x^2+4x-3=0 \]

3. Determinante (Δ):
   \[ \Delta = b^2-4ac = (4)^2 - 4\cdot(-1)\cdot(-3) = 16 - 12 = 4 \]

4. Raízes reais:
   \[ x=\frac{-b\pm\sqrt{\Delta}}{2a} = \frac{-4\pm 2}{-2} \] Logo, \(x_1=1\) e \(x_2=3\).

5. Esboço da parábola: como \(a=-1<0\), a parábola é côncava para baixo.
   Isso significa que a parábola está acima do eixo \(x\) entre as raízes e abaixo fora delas.

6. Sinal da parábola:

   • Para \(x<1\), \(f(x)<0\).
     
   • Para \(1\leqslant x\leqslant 3\), \(f(x)\geqslant 0\).
     
   • Para \(x>3\), \(f(x)<0\) novamente.

7. Conclusão (solução da inequação \(f(x)\geqslant 0\)):
   \[ x \in [1,3] \]

Diagrama na reta real:

Gráfico da parábola e estudo do sinal:

---

8 Inequações Produto

Forma geral:

\[ \boxed{(x-a)(x-b) < 0} \]

\[ \boxed{(x-a)(x-b) > 0} \]

\[ \boxed{(x-a)(x-b) \leqslant 0} \]

\[ \boxed{(x-a)(x-b) \geqslant 0} \]

A solução é determinada pelo sinal dos fatores em cada intervalo definido pelas raízes.

---

📌 Exemplo 1: Produto positivo Resolva: \[ x(x-1) > 0 \]

NotaResolução detalhada

• Raízes: \(x=0\) e \(x=1\).
  
• Intervalos: \((-\infty,0),\ (0,1),\ (1,+\infty)\).
  
• Teste de sinais:
  • Para \(x<0\): ambos fatores negativos ⇒ produto positivo.
    
  • Para \(0<x<1\): um positivo, outro negativo ⇒ produto negativo.
    
  • Para \(x>1\): ambos positivos ⇒ produto positivo.

✅ Solução: \((-\infty,0)\cup(1,+\infty)\).

---

📌 Exemplo 2: Produto negativo Resolva: \[ (x-1)(x+2) < 0 \]

NotaResolução detalhada

• Raízes: \(x=-2\) e \(x=1\).
  
• Intervalos: \((-\infty,-2),\ (-2,1),\ (1,+\infty)\).
  
• Teste de sinais:
  • Para \(x<-2\): ambos negativos ⇒ produto positivo.
    
  • Para \(-2<x<1\): sinais diferentes ⇒ produto negativo.
    
  • Para \(x>1\): ambos positivos ⇒ produto positivo.

✅ Solução: \((-2,1)\).

---

9 Inequações Quociente

Forma geral:

\[ \boxed{\dfrac{f(x)}{g(x)} < 0,\quad g(x)\neq 0} \]

\[ \boxed{\dfrac{f(x)}{g(x)} > 0,\quad g(x)\neq 0} \]

\[ \boxed{\dfrac{f(x)}{g(x)} \leqslant 0,\quad g(x)\neq 0} \]

\[ \boxed{\dfrac{f(x)}{g(x)} \geqslant 0,\quad g(x)\neq 0} \]

A solução é determinada pela tabela de sinais de numerador e denominador.

---

9.1 📌 O que são Assíntotas?

Nota📖 Definições

Seja uma função racional \(f(x)=\dfrac{p(x)}{q(x)}\).

• Assíntota vertical:
  Dizemos que \(x=a\) é uma assíntota vertical se:
  • \(q(a)=0\) (o denominador se anula em \(a\)); e
  • \(p(a)\ne0\) (o numerador não se anula em \(a\)).
    Nesse caso, \(f(x)\) não está definida em \(x=a\) e o gráfico da função se aproxima de uma linha vertical na reta \(x=a\).
• Assíntota horizontal:
  Dizemos que \(y=L\) é uma assíntota horizontal se \[ \lim_{x\to\pm\infty} f(x) = L. \] Isso significa que, para valores muito grandes (positivos ou negativos) de \(x\), o gráfico de \(f(x)\) se aproxima da reta horizontal \(y=L\).

📌 Estes conceitos serão explorados em detalhes no Módulo de Funções Racionais e, de forma mais rigorosa, no Módulo de Limites.

Dica🔎 Observação

• Nos problemas de inequações racionais, os valores que anulam o denominador nunca pertencem à solução, pois a expressão fica indefinida.
  
• Por isso, tratamos esses pontos como fronteiras da análise de sinais, e os chamamos de assíntotas verticais.
  
• Já as assíntotas horizontais ajudam a descrever o comportamento no infinito de uma função racional.

---

📌 Exemplo 1: Quociente positivo Resolva: \[ \frac{x+1}{x-3} > 0 \]

NotaResolução detalhada

• Zeros: numerador \(x=-1\).
  
• Assíntota: denominador \(x=3\).
  
• Intervalos: \((-\infty,-1),\ (-1,3),\ (3,+\infty)\).
  
• Sinais:
  • \((-\infty,-1)\): ambos negativos ⇒ quociente positivo.
    
  • \((-1,3)\): numerador positivo, denominador negativo ⇒ quociente negativo.
    
  • \((3,+\infty)\): ambos positivos ⇒ quociente positivo.

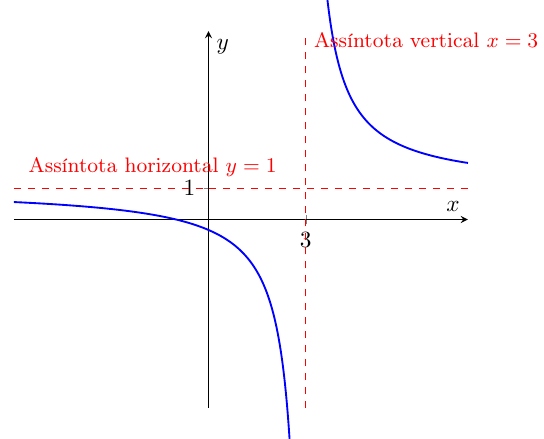
✅ Solução: \((-\infty,-1)\cup(3,+\infty)\).

---

📌 Exemplo 2: Quociente com mais fatores Resolva: \[ \frac{x^2-1}{x^2-3x} > 0 \]

NotaResolução detalhada

\[ \frac{(x-1)(x+1)}{x(x-3)} > 0, \quad x\neq 0,3. \]

• Zeros/assíntotas: \(-1,\,0,\,1,\,3\).
  
• Intervalos: \((-\infty,-1),\ (-1,0),\ (0,1),\ (1,3),\ (3,\infty)\).
  
• Teste de sinais:
  • \((-\infty,-1)\): positivo.
    
  • \((-1,0)\): negativo.
    
  • \((0,1)\): positivo.
    
  • \((1,3)\): negativo.
    
  • \((3,\infty)\): positivo.

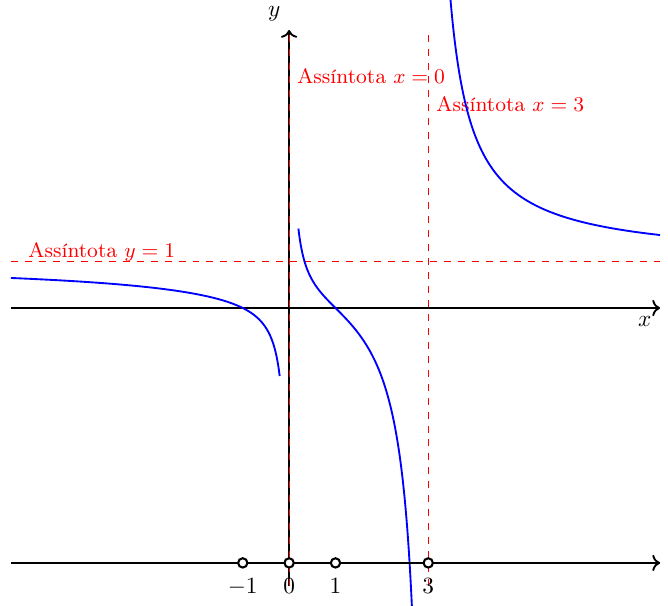
✅ Solução: \((-\infty,-1)\cup(0,1)\cup(3,\infty)\).

---

Nota📝 Exercícios Propostos

1. Represente na reta real:
   1. \((1,5]\)
      
   2. \((-\infty,-2)\)
      
   3. \([-3,3]\)
2. Resolva:
   1. \(3x+1\geqslant 7\)
      
   2. \(x^2-4\leqslant 0\)
      
   3. \((x-1)(x-4)<0\)

Importante✅ Gabarito

1. 1. bolinha aberta em 1, fechada em 5
      
   2. até \(-2\) aberto
      
   3. fechado de \(-3\) a \(3\)
2. 1. \([2,+\infty)\)
      
   2. \([-2,2]\)
      
   3. \((1,4)\)

---

9.2 🧠 Exercícios de Revisão

---

NotaExercício 1 — Desigualdade composta e intervalo

Resolva e escreva a solução em notação de intervalo: \[ 1<2x+3\le 9 \]

NotaResolução comentada

\[ \begin{aligned} 1<2x+3\le 9 &\iff 1-3<2x\le 9-3 \\ &\iff -2<2x\le 6 \\ &\iff -1<x\le 3 \quad (\text{dividir por }2>0) \end{aligned} \] Solução: \((-1,3]\).

---

NotaExercício 2 — Coeficiente negativo (troca de sinal)

Resolva: \[ -3x+5\ge 2 \]

NotaResolução comentada

\[ \begin{aligned} -3x+5\ge 2 &\iff -3x\ge -3 \\ &\iff x\le 1 \quad (\text{dividir por }-3<0 \Rightarrow \text{inverte}) \end{aligned} \] Solução: \((-\infty,1]\).

---

NotaExercício 3 — Inequação quadrática fatorável (< 0)

Resolva: \[ x^2-x-6<0 \]

NotaResolução comentada

Fatorando: \(x^2-x-6=(x-3)(x+2)\).
Raízes: \(x=-2\) e \(x=3\). Como \(a=1>0\), a parábola é côncava para cima.
Logo, \(f(x)<0\) entre as raízes: \[ x\in(-2,3). \] Solução: \((-2,3)\).

---

NotaExercício 4 — Inequação quadrática (raízes não inteiras) (≥ 0)

Resolva: \[ 2x^2+3x-2\ge 0 \]

NotaResolução comentada

Discriminante: \(\Delta=b^2-4ac=3^2-4\cdot2\cdot(-2)=9+16=25\).
Raízes: \[ x=\frac{-3\pm\sqrt{25}}{2\cdot2}=\frac{-3\pm5}{4}\;\Rightarrow\;x_1=-2,\;x_2=\tfrac12. \] Com \(a=2>0\), a parábola é côncava para cima; então \(f(x)\ge 0\) fora do intervalo entre as raízes (e inclui as raízes porque é \(\geqslant\)): \[ x\in(-\infty,-2]\cup\left[\tfrac12,\infty\right). \] Solução: \((-\infty,-2]\cup[0{,}5,\infty)\).

---

NotaExercício 5 — Operações com intervalos

Sejam \(A=(-\infty,4)\) e \(B=[1,7)\).
(a) \(A\cap B\) (b) \(A\cup B\)

NotaResolução comentada

• \(A\cap B\): pontos que estão nos dois.
  \(A\) vai até \(4\) (aberto), \(B\) começa em \(1\) (fechado) e vai até \(7\) (aberto).
  Interseção: de \(1\) até \(4\), incluindo \(1\) e excluindo \(4\): \([1,4)\).

• \(A\cup B\): pontos que estão em pelo menos um.
  A união cobre de \(-\infty\) até \(7\) aberto (porque \(B\) já cobre \([1,7)\) e \(A\) cobre \((-\infty,4)\)): \((-\infty,7)\).

Respostas: (a) \([1,4)\) (b) \((-\infty,7)\).

---

NotaExercício 6 — Resolva as inequações abaixo.

1. Produto: \(x(x-1)>0\)

NotaResolução comentada

Raízes em \(x=0\) e \(x=1\). Como o coeficiente líder é \(+1\), o produto é positivo fora do intervalo entre as raízes.
✅ Solução: \((-\infty,0)\cup(1,\infty)\).

---

2. Produto: \((x-1)(x+2)<0\)

NotaResolução comentada

Raízes em \(x=-2\) e \(x=1\). Coeficiente líder \(+1\) ⇒ negativo entre as raízes.
✅ Solução: \((-2,1)\).

---

3. Quadrática: \(x^2+4x-21>0\)

NotaResolução comentada

\(\Delta=4^2-4\cdot1\cdot(-21)=100\).
Raízes: \(x=\tfrac{-4\pm10}{2}\Rightarrow x=-7,\,3\).
Parábola abre para cima ⇒ \(>0\) fora.
✅ Solução: \((-\infty,-7)\cup(3,\infty)\).

---

4. Quadrática: \(2x^2+x<3\)

NotaResolução comentada

\(2x^2+x-3<0\).
\(\Delta=1+24=25\).
Raízes: \(x=\tfrac{-1\pm5}{4}\Rightarrow x=-\tfrac32,\,1\).
\(<0\) entre as raízes.
✅ Solução: \(\left(-\tfrac32,\,1\right)\).

---

5. Quadrática: \(4x^2+10x-6<0\)

NotaResolução comentada

\(\Delta=10^2-4\cdot4\cdot(-6)=196\).
Raízes: \(x=\tfrac{-10\pm14}{8}\Rightarrow x=-3,\,\tfrac12\).
\(<0\) entre as raízes.
✅ Solução: \((-3,\,\tfrac12)\).

---

6. Quadrática: \(x^2+2x+4>0\)

NotaResolução comentada

\(\Delta=2^2-4\cdot1\cdot4=-12<0\) e \(a=1>0\) ⇒ a expressão é sempre positiva.
✅ Solução: \(\mathbb{R}\).

---

NotaExercício 7 — Radicais reais (radicando ≥ 0)

1. \(\sqrt{4-x^2}\)

NotaResolução comentada

Precisamos \(4-x^2\ge0 \Rightarrow -2\le x\le 2\).
✅ Solução: \([-2,2]\).

---

2. \(\dfrac{1}{\sqrt{4-3x}}\)

NotaResolução comentada

O radicando deve ser positivo (e o denominador \(\ne0\)): \(4-3x>0 \Rightarrow x<\tfrac43\).
✅ Solução: \((-\infty,\tfrac43)\).

---

3. \(\dfrac{1}{\sqrt{x^2-x-12}}\)

NotaResolução comentada

Exigimos \(x^2-x-12>0\Rightarrow(x-4)(x+3)>0\) ⇒ fora das raízes.
✅ Solução: \((-\infty,-3)\cup(4,\infty)\).

---

NotaExercício 8 — Positividade de funções racionais

1. \(\dfrac{x}{x^2+4}>0\)

NotaResolução comentada

Denominador \(x^2+4>0\) para todo \(x\). Sinal da fração = sinal de \(x\).
✅ Solução: \((0,\infty)\).

---

2. \(\dfrac{x}{x^2-4}>0\)

NotaResolução comentada

Críticos: \(x=0,\pm2\) (em \(\pm2\) é indefinida). Tabela de sinais ⇒ positivo em \((-2,0)\) e \((2,\infty)\).
✅ Solução: \((-2,0)\cup(2,\infty)\).

---

3. \(\dfrac{x+1}{x-3}>0\)

NotaResolução comentada

Zero: \(-1\). Assíntota: \(3\). Sinais por intervalos ⇒ \((-\infty,-1)\) e \((3,\infty)\).
✅ Solução: \((-\infty,-1)\cup(3,\infty)\).

---

4. \(\dfrac{x^2-1}{x^2-3x}>0\)

NotaResolução comentada

\(\dfrac{(x-1)(x+1)}{x(x-3)}>0\), com \(x\ne0,3\). Críticos: \(-1,0,1,3\).
Sinais ⇒ \((-\infty,-1)\cup(0,1)\cup(3,\infty)\).
✅ Solução: \((-\infty,-1)\cup(0,1)\cup(3,\infty)\).

---

NotaExercício 9 — Descrever e diagramar o conjunto (em \(\mathbb{R}\))

1. \(x^2<4\)

NotaResolução comentada

\(-2<x<2\).
✅ Solução: \((-2,2)\).

---

2. \(x^2+3x-4>0\)

NotaResolução comentada

\((x+4)(x-1)>0\) ⇒ fora das raízes.
✅ Solução: \((-\infty,-4)\cup(1,\infty)\).

---

3. \(x^2+6x+8\le0\)

NotaResolução comentada

\((x+2)(x+4)\le0\) ⇒ entre as raízes, incluindo-as.
✅ Solução: \([-4,-2]\).

---

4. \(x^2<5x+14\)

NotaResolução comentada

\(x^2-5x-14<0\Rightarrow(x-7)(x+2)<0\) ⇒ entre as raízes.
✅ Solução: \((-2,7)\).

---

5. \(2x^2>x+6\)

NotaResolução comentada

\(2x^2-x-6>0\). \(\Delta=49\). Raízes: \(-\tfrac32\) e \(2\).
\(>0\) fora.
✅ Solução: \((-\infty,-\tfrac32)\cup(2,\infty)\).

---

6. \(6x^2+13x<5\)

NotaResolução comentada

\(6x^2+13x-5<0\). \(\Delta=289\). Raízes: \(-\tfrac52\) e \(\tfrac13\).
\(<0\) entre.
✅ Solução: \((-\tfrac52,\,\tfrac13)\).

---

7. \(x^3+3x^2>10x\)

NotaResolução comentada

\(x(x^2+3x-10)=x(x+5)(x-2)>0\).
Sinais por intervalos com críticos \(-5,0,2\) ⇒
✅ Solução: \((-5,0)\cup(2,\infty)\).

---

NotaExercício 10 — Resolva

1. \(-4<2-x<7\)

NotaResolução comentada

Somando \(-2\): \(-6<-x<5\). Multiplicando por \(-1\) (inverte): \(6>x>-5\).
✅ Solução: \((-5,6)\).

---

2. \(\dfrac{2x-1}{x}<3\)

NotaResolução comentada

\[ \frac{2x-1}{x}-3=\frac{-x-1}{x}<0 \ \Longleftrightarrow\ \frac{x+1}{x}>0. \] Críticos: \(-1,0\). Sinais ⇒ positivo em \((-\infty,-1)\) e \((0,\infty)\).
✅ Solução: \((-\infty,-1)\cup(0,\infty)\).

---

3. \(\dfrac{x}{x+2}<1\)

NotaResolução comentada

\[ \frac{x}{x+2}-1=\frac{-2}{x+2}<0 \ \Longleftrightarrow\ \frac{2}{x+2}>0 \] (numerador \(>0\)) ⇒ \(x+2>0 \Rightarrow x>-2\), com \(x\ne-2\).
✅ Solução: \((-2,\infty)\).

10 🔎 Quadro-Resumo — Módulo 1.3 (Ordem, Intervalos e Inequações)

---

Importante📖 Definições de Ordem em \(\mathbb{R}\)

• \(a<b \iff b-a>0\); \(a>b \iff a-b>0\).
• \(a\le b \iff (a<b \text{ ou } a=b)\); \(a\ge b \iff (a>b \text{ ou } a=b)\).
• Desigualdades estritas: \(<,>\). Não-estritas: \(\le,\ge\).

---

Nota📏 Propriedades de Ordem — Uso rápido

• Soma: \(a<b \Rightarrow a+c<b+c\).
• Produto por \(c>0\): preserva o sentido.
• Produto por \(c<0\): inverte o sentido.
• Transitividade: se \(a<b\) e \(b<c\), então \(a<c\).

---

Nota📦 Intervalos e Notação

• Aberto: \((a,b)=\{x\mid a<x<b\}\).
• Fechado: \([a,b]=\{x\mid a\le x\le b\}\).
• Semiabertos: \((a,b],\ [a,b)\).
• Infinitos: \((a,\infty),\ (-\infty,b),\ [a,\infty),\ (-\infty,b]\).

---

Importante🧮 Inequações Lineares (com (a))

Forma geral: \(\boxed{\,ax+b\ \{<,\le,>,\ge\}\ c\,}\)

NotaPasso a passo

1. Isolar o termo \(ax\) (somando/subtraindo dos dois lados).
   
2. Dividir por \(a\). Se \(a<0\), inverter a desigualdade.
   
3. Escrever a solução em intervalo e, se útil, testar um valor.
   

---

Importante🟦 Inequações Quadráticas

• Estudar o sinal de \(f(x)=ax^2+bx+c\) via raízes e concavidade.
• \(\Delta=b^2-4ac\).
  
• Se \(a>0\): \(f(x)\) é \(>0\) fora das raízes e \(<0\) entre.
  
• Se \(a<0\): comportamento invertido.

NotaPasso a passo

1. Resolver \(ax^2+bx+c=0\) (fatorar/BC).
   
2. Marcar as raízes na reta e a concavidade (sinal de \(a\)).
   
3. Escolher os intervalos que satisfazem \(>,\ge,<,\le\).
   
4. Incluir as raízes se a desigualdade for não-estrita (\(\ge,\le\)).
   

---

Nota✖️ Inequações Produto

• Tipo: \((x-a)(x-b)\ \{<,>,\le,\ge\}\ 0\).
  
• Regra: montar tabela de sinais dos fatores; o produto é \(+\) quando há número par de sinais negativos, e \(−\) quando ímpar.

NotaExemplo enxuto

\(x(x-1)>0 \Rightarrow (-\infty,0)\cup(1,\infty)\).
(Raízes \(0,1\); sinais: \(+,-,+\); queremos \(+\) → fora do intervalo.)

---

Nota➗ Inequações Quociente

• Tipo: \(\dfrac{f(x)}{g(x)}\ \{<,>,\le,\ge\}\ 0\), com \(g(x)\ne0\).
  
• Regra: sinais separam por zeros de \(f\) (numerador) e por assíntotas \(g=0\) (excluídas!).
  
• Quociente é \(+\) se numerador e denominador têm o mesmo sinal; \(−\) se têm sinais opostos.

NotaExemplo enxuto

\(\dfrac{x+1}{x-3}>0 \Rightarrow (-\infty,-1)\cup(3,\infty)\).
(Críticos \(-1\) [zero] e \(3\) [assíntota]; sinais: \(+,-,+\); queremos \(+\).)

---

Dica🧰 Checklist rápido para resolver

• Identifique tipo: linear / quadrática / produto / quociente.
  
• Encontre pontos críticos (raízes, assíntotas).
  
• Faça tabela de sinais por intervalos.
  
• Aplique a regra do sinal pedida (\(>,\ge,<,\le\)).
  
• Decida inclusão/exclusão das bordas.
  
• Escreva em notação de intervalo e teste um valor.

---

Nota⚠️ Erros comuns a evitar

• Esquecer de inverter a desigualdade ao dividir por número negativo.
  
• Incluir assíntotas (\(g(x)=0\)) em quocientes.
  
• Não verificar se a raiz entra na solução quando a relação é \(\ge\) ou \(\le\).
  
• Perder pontos críticos ao simplificar fatores comuns (anote restrições antes!).
  

---

11 🔗 Navegação

🎯 Próximo Post: 👉 1.3 Valor Absoluto e Inequações Modulares (Aprofundamento)

← Sumário do Curso · ← Cursos de Matemática · 🔝 Topo

---

Blog do Marcellini — Explorando a Matemática com Rigor e Beleza.

Nota

Criado por Blog do Marcellini com ❤️ e código.